
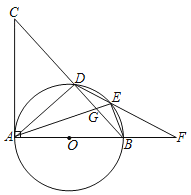
【题目】如图,AB是⊙O的直径,AC⊥AB,BC交⊙O于点D,点E在劣弧BD上,DE的延长线交AB的延长线于点F,连接AE交BD于点G.
(1)求证:∠AED=∠CAD;
(2)若点E是劣弧BD的中点,求证:ED2=EGEA;
(3)在(2)的条件下,若BO=BF,DE=2,求EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)4.
【解析】
(1)可得∠ADB=90°,证得∠ABD=∠CAD,∠AED=∠ABD,则结论得证;
(2)证得∠EDB=∠DAE,证明△EDG∽△EAD,可得比例线段![]() ,则结论得证;
,则结论得证;
(3)连接OE,证明OE∥AD,则可得比例线段![]() ,则EF可求出.
,则EF可求出.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°
∵AC⊥AB,
∴∠CAB=90°,
∴∠CAD+∠BAD=90°
∴∠ABD=∠CAD,
∵![]() =
=![]() ,
,
∴∠AED=∠ABD,
∴∠AED=∠CAD;
(2)证明:∵点E是劣弧BD的中点,
∴![]() ,
,
∴∠EDB=∠DAE,
∵∠DEG=∠AED,
∴△EDG∽△EAD,
∴![]() ,
,
∴ED2=EGEA;
(3)解:连接OE,
∵点E是劣弧BD的中点,
∴∠DAE=∠EAB,
∵OA=OE,
∴∠OAE=∠AEO,
∴∠AEO=∠DAE,
∴OE∥AD,
∴![]() ,
,
∵BO=BF=OA,DE=2,
∴![]() ,
,
∴EF=4.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
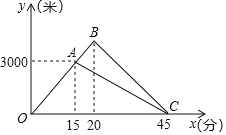
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB.CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
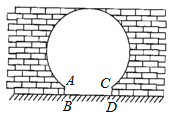
A.2米 B.2.5米 C.2.4米 D.2.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A、B、C三点的坐标分别为:A(1,4)、B(0,3)、C(3,0),若P为x轴上一点,且∠BPC=2∠ACB,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
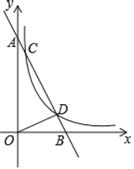
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,直线AB与反比例函数y=![]() (m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)分别求m、n的值;
(2)连接OD,求△ADO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
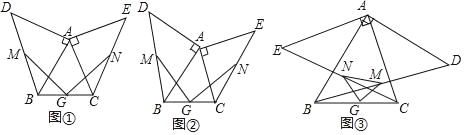
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax+c(a<0)的图象过点A(3,m).
(1)当a=﹣1,m=0时,求抛物线的顶点坐标_____;
(2)如图,直线l:y=kx+c(k<0)交抛物线于B,C两点,点Q(x,y)是抛物线上点B,C之间的一个动点,作QD⊥x轴交直线l于点D,作QE⊥y轴于点E,连接DE.设∠QED=β,当2≤x≤4时,β恰好满足30°≤β≤60°,a=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com