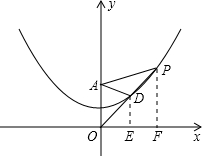
解:(1)如图,∵点A的坐标为(0,2),点P(m,n),
∴AP
2=m
2+(n-2)
2,①
∵点P(m,n)是抛物线
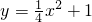
上的一个动点,
∴n=

m
2+1,
∴m
2=4n-4,②
由①②知,AP=n.
又∵PB⊥x轴,
∴PB=n,
∴PA=PB.
(2)①过点P作PB⊥x轴于B,由(1)得PA=PB,
所以要使AP+CP最小,只需当BP+CP最小,因此当C,P,B共线时取得,
此时点P的横坐标等于点C(2,5)的横坐标,
所以点P的坐标为(2,2);
②当点P在第一象限时,如图,作DE⊥x轴于E,作PF⊥x轴于F,
由(1)得:DA=DE,PA=PF
∵PA=2DA,∴PF=2DE,
∵△ODE∽△OPF,∴
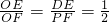
设P(m,
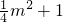
),则D(

,
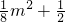
)
∴
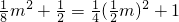
,解得

∵点D在抛物线
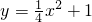
上,(负舍去)
此时P(

,3),直线OP的解析式为
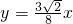
;
当P在第二象限时,
同理可求得直线OP的解析式为
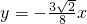
.
综上,所求直线OP的解析式为
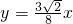
或
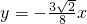
.
故答案为:=.
分析:(1)根据两点间的距离公式、二次函数图象上点的坐标特征推知PA=PB;
(2)过点P作PB⊥x轴于B,由(1)得PA=PB,所以要使AP+CP最小,只需当BP+CP最小,因此当C,P,B共线时,AP+PC取得最小值;
(3)分类讨论:当点P位于第一象限和第二象限.先以点P位于第一象限进行分析:如图,作DE⊥x轴于E,作PF⊥x轴于F,构建相似三角形△ODE∽△OPF,则该相似三角形的对应边成比例,即
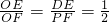
.故设设P(m,
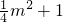
),则D(

,
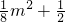
).由(1)中的结论得到等式
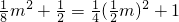
,据此可以求得点P的坐标为(

,3),则易求直线OP的解析式为
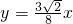
.
点评:本题考查了二次函数综合题.其中涉及到了二次函数图象上点的坐标特征,待定系数法求一次函数解析式以及轴对称--路线最短问题等知识点.在求有关动点问题时要注意分析题意分情况讨论结果.

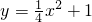 上的一个动点.
上的一个动点.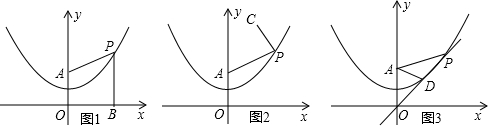
 解:(1)如图,∵点A的坐标为(0,2),点P(m,n),
解:(1)如图,∵点A的坐标为(0,2),点P(m,n),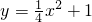 上的一个动点,
上的一个动点, m2+1,
m2+1,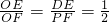
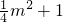 ),则D(
),则D( ,
,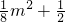 )
)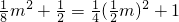 ,解得
,解得
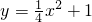 上,(负舍去)
上,(负舍去) ,3),直线OP的解析式为
,3),直线OP的解析式为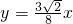 ;
;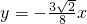 .
.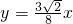 或
或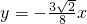 .
.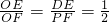 .故设设P(m,
.故设设P(m,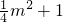 ),则D(
),则D( ,
,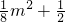 ).由(1)中的结论得到等式
).由(1)中的结论得到等式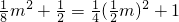 ,据此可以求得点P的坐标为(
,据此可以求得点P的坐标为( ,3),则易求直线OP的解析式为
,3),则易求直线OP的解析式为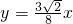 .
.

 阅读快车系列答案
阅读快车系列答案
 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=