
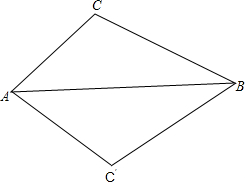
 如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.
如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.  培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:填空题
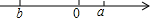 已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.
已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 有一组邻边相等、一个角是直角的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
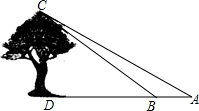 大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 36 | B. | 46 | C. | -26 | D. | -46 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
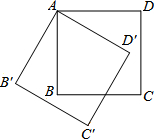 如图,将边长为2cm的正方形ABCD绕点A顺时针旋转到AB′C′D′的位置,∠B′AD=120°,则C点运动到C′点的路径长为$\frac{\sqrt{2}}{3}$πcm.
如图,将边长为2cm的正方形ABCD绕点A顺时针旋转到AB′C′D′的位置,∠B′AD=120°,则C点运动到C′点的路径长为$\frac{\sqrt{2}}{3}$πcm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com