
”¾ĢāÄæ”æČēĶ¼¢Ł£¬Ö±Ļßy=![]() x+4½»ÓŚxÖįÓŚµćA£¬½»yÖįÓŚµćC£¬¹żA”¢CĮ½µćµÄÅ×ĪļĻßF1½»xÖįÓŚĮķŅ»µćB£Ø1£¬0£©£®
x+4½»ÓŚxÖįÓŚµćA£¬½»yÖįÓŚµćC£¬¹żA”¢CĮ½µćµÄÅ×ĪļĻßF1½»xÖįÓŚĮķŅ»µćB£Ø1£¬0£©£®
£Ø1£©ĒóÅ×ĪļĻßF1Ėł±ķŹ¾µÄ¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©ČōµćMŹĒÅ×ĪļĻßF1Ī»ÓŚµŚ¶žĻóĻŽĶ¼ĻóÉĻµÄŅ»µć£¬ÉčĖıߊĪMAOCŗĶ”÷BOCµÄĆ껿·Ö±šĪŖSĖıߊĪMAOCŗĶS”÷BOC£¬¼ĒS=SĖıߊĪMAOC©S”÷BOC£¬ĒóS×ī“󏱵ćMµÄ×ų±ź¼°SµÄ×ī“óÖµ£»
£Ø3£©ČēĶ¼¢Ś£¬½«Å×ĪļĻßF1ŃŲyÖį·ÕŪ²¢”°ø“ÖĘ”±µĆµ½Å×ĪļĻßF2£¬µćA”¢BÓė£Ø2£©ÖŠĖłĒóµÄµćMµÄ¶ŌÓ¦µć·Ö±šĪŖA”䔢B”䔢M”䣬¹żµćM”ä×÷M”äE”ĶxÖįÓŚµćE£¬½»Ö±ĻßA”äCÓŚµćD£¬ŌŚxÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌA”䔢D”¢PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AB”äCĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ(1)y=©![]() x2©
x2©![]() x+4;(2)SÓŠ×ī“óÖµĪŖ
x+4;(2)SÓŠ×ī“óÖµĪŖ![]() £¬“ĖŹ±£¬M£Ø©
£¬“ĖŹ±£¬M£Ø©![]() £¬5£©£»µćPµÄ×ų±źĪŖ£Ø2£¬0£©»ņ£Ø©
£¬5£©£»µćPµÄ×ų±źĪŖ£Ø2£¬0£©»ņ£Ø©![]() £¬0£©£®
£¬0£©£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻŅ»“ĪŗÆŹżµÄ½āĪöŹ½y=![]() x+4æÉĒó³öµćA”¢CµÄ×ų±ź£¬ŌŁ°ŃA”¢B”¢CµÄ×ų±ź“śČė£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹżµÄ½āĪöŹ½£»£Ø2£©ÓÉÓŚMŌŚÅ×ĪļĻßF1ÉĻ£¬ĖłŅŌæÉÉčM£Øa£¬©
x+4æÉĒó³öµćA”¢CµÄ×ų±ź£¬ŌŁ°ŃA”¢B”¢CµÄ×ų±ź“śČė£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹżµÄ½āĪöŹ½£»£Ø2£©ÓÉÓŚMŌŚÅ×ĪļĻßF1ÉĻ£¬ĖłŅŌæÉÉčM£Øa£¬©![]() a2©
a2©![]() a+4£©£¬·Ö±š¼ĘĖćSĖıߊĪMAOCŗĶS”÷BOC£¬¹żµćM×÷MD”ĶxÖįÓŚµćD£¬ŌņSĖıߊĪMAOCµÄÖµµČÓŚ”÷ADMµÄĆ껿ÓėĢŻŠĪDOCMµÄĆ껿֮ŗĶ£¬ĒóµĆSĖıߊĪMAOCµÄÖµ£¬ŌŁÓÉS=SĖıߊĪMAOC©S”÷BOC±ķŹ¾³öSÓėaµÄ¶ž“ĪŗÆŹż¹ŲĻµ£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ¼“æɵĆS×ī“󏱵ćMµÄ×ų±ź¼°SµÄ×ī“óÖµ£»£Ø3£©ÓÉÓŚ²»Č·¶ØµćPµÄ¾ßĢåĪ»ÖĆ£¬ĖłŅŌŠčŅŖ½«µćPµÄĪ»ÖĆ½ųŠŠ·ÖĄąĢÖĀŪ£¬µ±µćPŌŚA”äµÄÓŅ±ßŹ±£¬“ĖĒéæöŹĒ²»“ęŌŚ£»µ±µćPŌŚA”äµÄ×ó±ßŹ±£¬“ĖŹ±”ĻDA”äP=”ĻCAB”䣬ČōŅŌA”䔢D”¢PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AB”äCĻąĖĘ£¬Ōņ·ÖĪŖŅŌĻĀĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ£ŗ¢Ł
a+4£©£¬·Ö±š¼ĘĖćSĖıߊĪMAOCŗĶS”÷BOC£¬¹żµćM×÷MD”ĶxÖįÓŚµćD£¬ŌņSĖıߊĪMAOCµÄÖµµČÓŚ”÷ADMµÄĆ껿ÓėĢŻŠĪDOCMµÄĆ껿֮ŗĶ£¬ĒóµĆSĖıߊĪMAOCµÄÖµ£¬ŌŁÓÉS=SĖıߊĪMAOC©S”÷BOC±ķŹ¾³öSÓėaµÄ¶ž“ĪŗÆŹż¹ŲĻµ£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ¼“æɵĆS×ī“󏱵ćMµÄ×ų±ź¼°SµÄ×ī“óÖµ£»£Ø3£©ÓÉÓŚ²»Č·¶ØµćPµÄ¾ßĢåĪ»ÖĆ£¬ĖłŅŌŠčŅŖ½«µćPµÄĪ»ÖĆ½ųŠŠ·ÖĄąĢÖĀŪ£¬µ±µćPŌŚA”äµÄÓŅ±ßŹ±£¬“ĖĒéæöŹĒ²»“ęŌŚ£»µ±µćPŌŚA”äµÄ×ó±ßŹ±£¬“ĖŹ±”ĻDA”äP=”ĻCAB”䣬ČōŅŌA”䔢D”¢PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AB”äCĻąĖĘ£¬Ōņ·ÖĪŖŅŌĻĀĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ£ŗ¢Ł![]() £»¢Ś
£»¢Ś![]() £¬·Ö±šĒóµĆµćPµÄ×ų±ź¼“æÉ.
£¬·Ö±šĒóµĆµćPµÄ×ų±ź¼“æÉ.
ŹŌĢā½āĪö£ŗ£Ø1£©Įīy=0“śČėy=![]() x+4£¬
x+4£¬
”ąx=©3£¬
A£Ø©3£¬0£©£¬
Įīx=0£¬“śČėy=![]() x+4£¬
x+4£¬
”ąy=4£¬
”ąC£Ø0£¬4£©£¬
ÉčÅ×ĪļĻßF1µÄ½āĪöŹ½ĪŖ£ŗy=a£Øx+3£©£Øx©1£©£¬
°ŃC£Ø0£¬4£©“śČėÉĻŹ½µĆ£¬a=©![]() £¬
£¬
”ąy=©![]() x2©
x2©![]() x+4£¬
x+4£¬
£Ø2£©ČēĶ¼¢Ł£¬ÉčµćM£Øa£¬©![]() a2©
a2©![]() a+4£©
a+4£©
ĘäÖŠ©3£¼a£¼0
”ßB£Ø1£¬0£©£¬C£Ø0£¬4£©£¬
”ąOB=1£¬OC=4
”ąS”÷BOC=![]() OBOC=2£¬
OBOC=2£¬
¹żµćM×÷MD”ĶxÖįÓŚµćD£¬
”ąMD=©![]() a2©
a2©![]() a+4£¬AD=a+3£¬OD=©a£¬
a+4£¬AD=a+3£¬OD=©a£¬
”ąSĖıߊĪMAOC=![]() ADMD+
ADMD+![]() £ØMD+OC£©OD
£ØMD+OC£©OD
=![]() ADMD+
ADMD+![]() ODMD+
ODMD+![]() ODOC
ODOC
=![]() +
+![]()
=![]() +
+![]()
=![]() ”Į3£Ø©
”Į3£Ø©![]() a2©
a2©![]() a+4£©+
a+4£©+![]() ”Į4”Į£Ø©a£©
”Į4”Į£Ø©a£©
=©2a2©6a+6
”ąS=SĖıߊĪMAOC©S”÷BOC
=£Ø©2a2©6a+6£©©2
=©2a2©6a+4
=©2£Øa+![]() £©2+
£©2+![]()
”ąµ±a=©![]() Ź±£¬
Ź±£¬
SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ![]()
“ĖŹ±£¬M£Ø©![]() £¬5£©£»
£¬5£©£»
£Ø3£©ČēĶ¼¢Ś£¬ÓÉĢāŅāÖŖ£ŗM”ä£Ø![]() £©£¬B”ä£Ø©1£¬0£©£¬A”ä£Ø3£¬0£©
£©£¬B”ä£Ø©1£¬0£©£¬A”ä£Ø3£¬0£©
”ąAB”ä=2
ÉčÖ±ĻßA”äCµÄ½āĪöŹ½ĪŖ£ŗy=kx+b£¬
°ŃA”ä£Ø3£¬0£©ŗĶC£Ø0£¬4£©“śČėy=kx+b£¬
µĆ£ŗ![]() £¬
£¬
”ą
”ąy=©![]() x+4£¬
x+4£¬
Įīx=![]() “śČėy=©
“śČėy=©![]() x+4£¬
x+4£¬
”ąy=2
”ą![]()
Óɹ“¹É¶ØĄķ·Ö±šæÉĒóµĆ£ŗAC=5£¬DA”ä=![]()
ÉčP£Øm£¬0£©
µ±m£¼3Ź±£¬
“ĖŹ±µćPŌŚA”äµÄ×ó±ß£¬
”ą”ĻDA”äP=”ĻCAB”䣬
µ±![]() =
=![]() Ź±£¬”÷DA”äP”×”÷CAB”䣬
Ź±£¬”÷DA”äP”×”÷CAB”䣬
“ĖŹ±£¬![]() =
=![]() £Ø3©m£©£¬
£Ø3©m£©£¬
½āµĆ£ŗm=2£¬
”ąP£Ø2£¬0£©
µ±![]() =
=![]() Ź±£¬”÷DA”äP”×”÷B”äAC£¬
Ź±£¬”÷DA”äP”×”÷B”äAC£¬
“ĖŹ±£¬![]() =
=![]() £Ø3©m£©
£Ø3©m£©
m=©![]() £¬
£¬
”ąP£Ø©![]() £¬0£©
£¬0£©
µ±m£¾3Ź±£¬
“ĖŹ±£¬µćPŌŚA”äÓŅ±ß£¬
ÓÉÓŚ”ĻCB”äO”Ł”ĻDA”äE£¬
”ą”ĻAB”äC”Ł”ĻDA”äP
”ą“ĖĒéæö£¬”÷DA”äPÓė”÷B”äAC²»ÄÜĻąĖĘ£¬
×ŪÉĻĖłŹö£¬µ±ŅŌA”䔢D”¢PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AB”äCĻąĖĘŹ±£¬µćPµÄ×ų±źĪŖ£Ø2£¬0£©»ņ£Ø©![]() £¬0£©£®
£¬0£©£®



 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŅ»“ĪŗÆŹży=kx+b£¬µ±x=2Ź±yµÄÖµŹĒ©1£¬µ±x=©1Ź±yµÄÖµŹĒ5£®
£Ø1£©Ēó“ĖŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ČōµćP£Øm£¬n£©ŹĒ“ĖŗÆŹżĶ¼ĻóÉĻµÄŅ»µć£¬©3”Üm”Ü2£¬ĒónµÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōÅ×ĪļĻßL£ŗy=ax2+bx+c£Øa£¬b£¬cŹĒ³£Źż£¬abc”Ł0£©ÓėÖ±Ļßl¶¼¾¹żyÖįÉĻµÄŅ»µćP£¬ĒŅÅ×ĪļĻßLµÄ¶„µćQŌŚÖ±ĻßlÉĻ£¬Ōņ³Ę“ĖÖ±ĻßlÓėøĆÅ×ĪļĻßL¾ßÓŠ”°Ņ»“ųŅ»Ā·”±¹ŲĻµ£®“ĖŹ±£¬Ö±Ļßl½Š×öÅ×ĪļĻßLµÄ”°“ųĻß”±£¬Å×ĪļĻßL½Š×öÖ±ĻßlµÄ”°Ā·Ļß”±£®
£Ø1£©ČōÖ±Ļßy=mx+1ÓėÅ×ĪļĻßy=x2©2x+n¾ßÓŠ”°Ņ»“ųŅ»Ā·”±¹ŲĻµ£¬Ēóm£¬nµÄÖµ£»
£Ø2£©Čōij”°Ā·Ļß”±LµÄ¶„µćŌŚ·“±ČĄżŗÆŹży=![]() µÄĶ¼ĻóÉĻ£¬ĖüµÄ”°“ųĻß”±lµÄ½āĪöŹ½ĪŖy=2x©4£¬Ēó“Ė”°Ā·Ļß”±LµÄ½āĪöŹ½£»
µÄĶ¼ĻóÉĻ£¬ĖüµÄ”°“ųĻß”±lµÄ½āĪöŹ½ĪŖy=2x©4£¬Ēó“Ė”°Ā·Ļß”±LµÄ½āĪöŹ½£»
£Ø3£©µ±³£ŹżkĀś×ć![]() ”Ük”Ü2Ź±£¬ĒóÅ×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kµÄ”°“ųĻß”±lÓėxÖį£¬yÖįĖłĪ§³ÉµÄČż½ĒŠĪĆ껿µÄȔֵ·¶Ī§£®
”Ük”Ü2Ź±£¬ĒóÅ×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kµÄ”°“ųĻß”±lÓėxÖį£¬yÖįĖłĪ§³ÉµÄČż½ĒŠĪĆ껿µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹŠŹµŃé֊ѧѧɜ²½ŠŠµ½½¼ĶāĀĆÓĪ£®ĘߣØ1£©°ąŃ§Éś×é³ÉĒ°¶Ó£¬²½ŠŠĖŁ¶ČĪŖ4Ē§Ć×/Ź±£¬ĘߣØ2£©°ąŃ§Éś×é³Éŗó¶Ó£¬ĖŁ¶ČĪŖ 6Ē§Ć×/Ź±£®Ē°¶Ó³ö·¢1Š”Ź±ŗó£¬ŗó¶Ó²Å³ö·¢£¬Ķ¬Ź±ŗó¶ÓÅÉŅ»ĆūĮŖĀēŌ±Ęļ×ŌŠŠ³µŌŚĮ½¶ÓÖ®¼ä²»¼ä¶ĻµŲĄ“»Ų½ųŠŠĮŖĀē£¬ĖūĘļ³µµÄĖŁ¶ČĪŖ12Ē§Ć×/Ź±£®
£Ø1£©ŗó¶Ó×·ÉĻĒ°¶ÓŠčŅŖ¶ą³¤Ź±¼ä£æ
£Ø2£©ŗó¶Ó×·ÉĻĒ°¶ÓŹ±¼äÄŚ£¬ĮŖĀēŌ±×ßµÄĀ·³ĢŹĒ¶ąÉŁ£æ
£Ø3£©Į½¶ÓŗĪŹ±Ļą¾ą2Ē§Ć×£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚČĪŅāŹµŹż¶Ō(a£¬b)ŗĶ(c£¬d)£¬¹ę¶ØŌĖĖć”°*”±ĪŖ(a£¬b)*(c£¬d)=(ac£¬bd)£»ŌĖĖć”°Ø”±ĪŖ(a£¬b)Ø(c£¬d)=(a+c£¬b+d)£®Čō(1£¬2)*(p£¬q)=(2£¬£4)£¬Ōņ(1£¬2)Ø(p£¬q)=________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©¼ĘĖć£ŗ2a2a4©(2a2)3+7a6
£Ø2£©ŅņŹ½·Ö½ā£ŗ3x3©12x2+12x
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
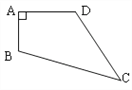
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼9£¬ĖıߊĪABCDÖŠ£¬AB=3cm£¬AD=4cm£¬BC=13cm£¬CD=12cm£¬ĒŅ”ĻA=90”ć£¬ŌņĖıߊĪABCDµÄĆ껿____________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ“śŹżŹ½a2+aµÄÖµŹĒ1£¬Ōņ“śŹżŹ½2a2+2a+2018ÖµŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com