
| A. | $\sqrt{{a}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{a+1}$a<-1时二次根式无意义,故A错误;
B、$\sqrt{\frac{1}{2}}$被开方数含有分母,故B错误;
C、$\sqrt{8}$被开方数不含能开得尽方的因数或因式,故C错误;
D、$\sqrt{10}$被开方数不含分母;被开方数不含能开得尽方的因数或因式,故D正确;
故选:D.
点评 本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
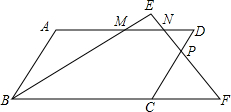 如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.
如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.
在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
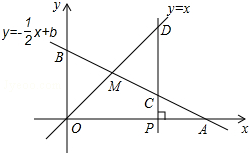 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.
如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com