

分析 (1)直接根据勾股定理可求出AB的长;
(2)△ACP为等腰三角形,分三种情况探讨:①CP=CA,②AP=AC,③PA=PC;逐一分析找出答案即可.
解答 解:(1)∵∠ABC=90°,BC=6cm,AC=10cm,
∴AB=$\sqrt{{AC}^{2}-{BC}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8cm;
(2)①如图1,若CP=CA,
则:BP=CP+BC=6+10=16或BP=CP-BC=10-6=4,
即2t=16,t=8或2t=4,t=2;
②如图2,若AP=AC,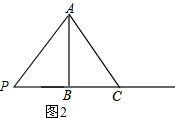
则:AB垂直平分PC,BP=BC=6,
即2t=6,t=3;
③若PA=PC,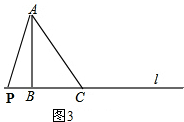
则P在AC的垂直平分线上,所以P在B左侧,
PB=2t,BC=6,
∴t=8,PA=2t+6,
∵∠ABP=90°,
∴AP2=AB2+BP2,
即(2t+6)2=(2t)2+82,
解得t=$\frac{7}{6}$;
综上所述,当点P向左运动$\frac{7}{6}$s、2s、3s或向右运动8s时,△ACP为等腰三角形.
点评 此题考查的是勾股定理、等腰三角形的性质等知识,在解答此题时要注意进行分类讨论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一架云梯长25米,斜靠在一面墙上,梯子靠墙的一端距地面24米.
如图,一架云梯长25米,斜靠在一面墙上,梯子靠墙的一端距地面24米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,连结EF.求证:
如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,连结EF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
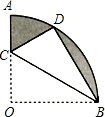 如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为π-$\frac{4\sqrt{3}}{3}$.
如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为π-$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com