
【题目】在平面直角坐标系 xoy 中,已知点 A 的坐标为(-2,0).
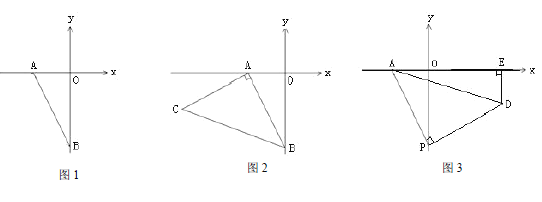
(1)如图 1,当点 B 的坐标为(0,-4)时,则△AOB 的面积是 ;
(2)如图 2,在(1)的条件下,过点 A 作 AC⊥AB,且使 AC=AB,求第三象限内的点 C 的坐标;
(3)如图 3,P 为 y 轴负半轴上一点,过点 P 作 PD⊥PA,且使 PD=PA,过第四象限内的点 D 作 DE⊥x 轴于 E,试判断 OP-DE 的值是否发生变化.若不发生变化,请求其值;若发生变化,请说明理由.
【答案】(1)4;(2)点C坐标为(-6,-2);(3)![]() 的值不发生变化,其值为2, 证明见解析
的值不发生变化,其值为2, 证明见解析
【解析】
(1)由A(-2,0),B(0,-4)可得OA、OB的长度,利用三角形的面积公式进行计算即可得出答案;
(2)作CD⊥AD,易证∠ACD=∠OAB,即可求证△ACD≌△BAO,可得AD=OB,CD=OA即可解题;
(3)作DF⊥OP,易证∠APO=∠PDF,即可证明△AOP≌△PFD,可得AO=PF,DE=OF,即可解题.
(1)∵A(-2,0),B(0,-4)
∴OA=2,OB=4
∴△AOB 的面积是:![]()
故答案为:4
(2)如图,
过点C作CD⊥AD,
∴∠ADC=∠AOB=90°,
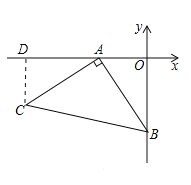
∵∠CAD+∠ACD=90°,∠CAD+∠OAB=90°,
∴∠ACD=∠OAB,
在△ACD和△BAO中,
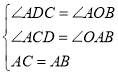
∴△ACD≌△BAO,(AAS)
∴AD=OB,CD=OA,
∴OD=6,CD=2
∴点C坐标为(-6,-2);
(3) OP-DE的值不发生变化,其值为2,理由如下:
作DF⊥OP,
∴∠AOP=∠PFD=90°,
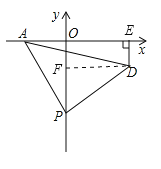
∵∠APO+∠DPF=90°,∠PDF+∠DPF=90°,
∴∠APO=∠PDF,
在△AOP和△PFD中,
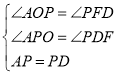
∴△AOP≌△PFD,(AAS)
∴AO=PF,
∵DE⊥x轴
∴∠OED=90°
∴∠OED=∠FOE=∠OFD=90°
∴四边形OFDE是矩形
∴DE=OF,
∴OP-DE=OP-OF=FP=AO=2


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】已知正比例函数和反比例函数的图象都经过点 A(3,3).
(1)求正比例函数和反比例函数的解析式;
(2)把直线 OA 向下平移后得到直线 l,与反比例函数的图象交于点 B(6,m),求 m 的值和直线 l 的解 析式;
(3)在(2)中的直线 l 与 x 轴、y 轴分别交于 C、D,求四边形 OABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火车、运输工具可供选择,两种运输工具的主要参考数据如下:
运输工具 | 途中平均速度(单位:千米/时) | 途中平均费用(单位:元/千米) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
汽车 | 75 | 8 | 2 | 1000 |
火车 | 100 | 6 | 4 | 2000 |
若这批水果在运输过程中(含装卸时间)的损耗为150元/时,设运输路程为x(![]() )千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
)千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
(1)分别求出y1、y2与x的关系式;
(2)那么你认为采用哪种运输工具比较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y= ax2+bx+c开口向下,并且经过A(0,1)和M(2,-3)两点。
(1)若抛物线的对称轴为直线x= -1,求此抛物线的解析式;
(2)如果抛物线的对称轴在y轴的左侧,试求a的取值范围;
(3)如果抛物线与x轴交于B、C两点,且∠BAC=90,求此时a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com