
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.

(1)求证:DE=AB.
(2)以D为圆心, DE为半径作圆弧交AD于点G.若BF=FC=1,试求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由矩形的性质得出∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,得出∠EAD=∠AFB,由AAS证明△ADE≌△FAB,得出对应边相等即可;
(2)连接DF,先证明△DCF≌△ABF,得出DF=AF,再证明△ADF是等边三角形,得出∠DAE=60°,
∠ADE=30°,由AE=BF=1,根据三角函数得出DE,由弧长公式即可求出![]() 的长.
的长.
试题解析:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,
∴∠EAD=∠AFB,
∵DE⊥AF,
∴∠AED=90°=∠B,
∵AF=DA
∴△ADE≌△FAB(AAS),
∴DE=AB;
(2)连接DF,如图所示:
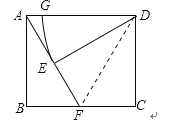
在△DCF和△ABF中,
DC=AB∠C=∠BFC=BF,
∴△DCF≌△ABF(SAS),
∴DF=AF,
∵AF=AD,
∴DF=AF=AD,
∴△ADF是等边三角形,
∴∠DAE=60°,
∵DE⊥AF,
∴∠AED=90°,
∴∠ADE=30°,
∵△ADE≌△FAB,
∴AE=BF=1,
∴DE=![]() AE=
AE=![]() ,
,
∴![]() 的长=30×π×3180=
的长=30×π×3180=![]() .
.


科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°
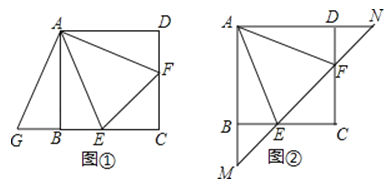
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2
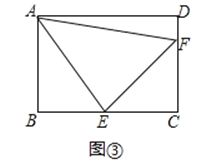
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )
A. 800(1+a%)2=578 B. 800(1-a%)2="578" C. 800(1-2a%)=578 D. 800(1-a2%)=578
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年师大附中秋季运动会,为了准备入场式,初一年级某班买了两种布料共28米,花了88元.其中黄布料每米3元,红布料每米3.5元,该班两种布料各买了多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com