
分析 (1)将特殊角的三角函数值代入,再根据实数的混合运算顺序和法则计算可得;
(2)整理成一般式后,公式法求解可得.
解答 解:(1)原式=1-$\sqrt{2}$+$\sqrt{2}$-|$\sqrt{3}$-2$\sqrt{3}$|
=1-$\sqrt{3}$;
(2)原式变为x2-4x-3=0,
∵a=1,b=-4,c=-3,
∴△=16-4×1×(-3)=28>0,
则x=$\frac{4±2\sqrt{7}}{2}$=2$±\sqrt{7}$,
∴x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$.
点评 本题主要考查特殊角的三角函数值、实数的混合运算及解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
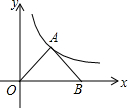 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
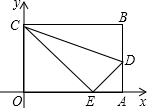 如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com