
����Ŀ������������ǰ����һ�ΰְ�ȥ���й����˴�С����������ͬ�Ļ������ӺͶ�ɳ�������ɣ����벻���ĺ��У���ʱ���ȡ���������ӵĸ���Ϊ![]() �����跢��С��ϲ���ԵĻ�������ƫ�٣��ڶ���������ȥ����ͬ����
�����跢��С��ϲ���ԵĻ�������ƫ�٣��ڶ���������ȥ����ͬ����![]() ֻ�������Ӻ�
ֻ�������Ӻ�![]() ֻ��ɳ���ӷ���ͬһ���У���ʱ���ȡ���������ӵĸ���Ϊ
ֻ��ɳ���ӷ���ͬһ���У���ʱ���ȡ���������ӵĸ���Ϊ![]() ��
��
![]() ��������һ�ΰְ���Ļ������ӺͶ�ɳ���Ӹ��ж���ֻ��
��������һ�ΰְ���Ļ������ӺͶ�ɳ���Ӹ��ж���ֻ��
![]() ������Ӻ���ȡ����������
������Ӻ���ȡ����������![]() ֻ����ɳ����
ֻ����ɳ����![]() ֻ��үү�����̺�����С���Ӻ��в��Żص���ȡ
ֻ��үү�����̺�����С���Ӻ��в��Żص���ȡ![]() ֻ����ǡ�л������ӡ���ɳ���Ӹ�
ֻ����ǡ�л������ӡ���ɳ���Ӹ�![]() ֻ�ĸ����Ƕ��٣�������ĸ�����ֱ�ʾ��ɳ���Ӻͻ������ӣ������巨���㣩
ֻ�ĸ����Ƕ��٣�������ĸ�����ֱ�ʾ��ɳ���Ӻͻ������ӣ������巨���㣩
���𰸡���1����һ�ΰְ�����4ֻ����������8ֻ��ɳ��������2��![]() ��
��
��������
��1��������ϵΪ��ԭ���Ļ�����������ԭ������������=![]() �������Ļ����������º�������������=
�������Ļ����������º�������������=![]() ��
��
��2���оٳ��������������������ռ��������ĸ��������
��1�����һ�ΰְ�����xֻ����������yֻ��ɳ�����������������
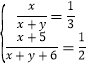 �������
�������![]() ��
��
������ó���x+y��0��x+y+6��0����x=4��y=8��ԭ���̵ĸ���
������һ�ΰְ�����4ֻ����������8ֻ��ɳ������
��2�������л�������9ֻ����ɳ����9ֻ����үү�����̺������л�������5ֻ����ɳ����3ֻ��
�Ƕ�ɳ����a��b��c����������1��2��3��4��5��ǡ�û������ӡ���ɳ���Ӹ�1ֻ�ĸ���Ϊ![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �DZ߳�Ϊ6�ĵȱ������Σ�
�DZ߳�Ϊ6�ĵȱ������Σ�![]() ��
��![]() ����һ���㣬��
����һ���㣬��![]() ��
��![]() �˶�����
�˶�����![]() ��
��![]() ���غϣ���
���غϣ���![]() ��
��![]() �ӳ�����һ���㣬���
�ӳ�����һ���㣬���![]() ͬʱ����ͬ���ٶ���
ͬʱ����ͬ���ٶ���![]() ��
��![]() �ӳ��߷����˶���
�ӳ��߷����˶���![]() ����
����![]() �غϣ�����
�غϣ�����![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() .
.

��1����![]() ʱ����
ʱ����![]() �ij���
�ij���
��2�����˶��������߶�![]() �ij��Ƿ����仯��������䣬����߶�
�ij��Ƿ����仯��������䣬����߶�![]() �ij�����������ı䣬��˵������.
�ij�����������ı䣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF�ڵ�G�����н��ۣ���![]() ����AG=
����AG=![]() GC����BE+DF=EF����
GC����BE+DF=EF����![]() .������ȷ���ǣ� ��
.������ȷ���ǣ� ��

A.�٢ڢ�B.�٢ۢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ֱ��y��x+2����������ֱ���A��B���㣬��C��OB���е㣬D��E�ֱ���ֱ��AB��y���ϵĶ��㣬����CDE�ܳ���Сʱ����D������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���![]() ������
������![]() �Ϸֱ�ȡ��
�Ϸֱ�ȡ��![]() ��
��![]() ��ʹ
��ʹ![]() ����ʱǡ��
����ʱǡ��![]() ����
����![]() �Ķ�����____________.
�Ķ�����____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1�����������ABC(�����������ߵĽ����������)�Ķ���A��C������ֱ�Ϊ(��4��5)��(��1��3).
(1)��������ABC����y��ԳƵġ�A1B1C1��
(2)��A1B1C1�������______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�͡�DEFΪ���������Σ�AB��AC��DE��DF����BAC����EDF����E��AB�ϣ���F������AC��.
(1)��ͼ1������BAC��60������F���C�غϣ�
����֤��AF��AE+AD.
����֤��AD��BC.
(2)��ͼ2����AD��AB����ô�߶�AF��AE��BC֮�����������������ϵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ���ڣ�����P����ABC���������е������������������γɵ������ζ��ǵ��������Σ���Ƶ�P����ABC�������.
��1����ͼ1��������ABC�������P���߹���ͼ����д������������ͼ�ۼ���.

��2����ͼ2������ABC�У���A=80����AB=AC��������ABC�����������P ���߹���ͼ����д������������ͼ�ۼ�������ֱ��д����BPC�Ķ����� .

��3���ȱ������ε������ĸ����У� ��
A.2 B.6 C.10 D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=60������P�ǡ�AOB�ڵĶ�����OP=![]() ������M��N�ֱ�������OA��OB�����ڵ�O�Ķ��㣬����PMN�ܳ�����Сֵ�ǣ�������
������M��N�ֱ�������OA��OB�����ڵ�O�Ķ��㣬����PMN�ܳ�����Сֵ�ǣ�������

A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com