
 让我们来共同探究“三角形的角平分线”的特殊性质:
让我们来共同探究“三角形的角平分线”的特殊性质:分析 (1)过点D作DE⊥AB,DF⊥AC,根据角平分线的性质,得出DE=DF,再根据三角形的面积计算公式,得出$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{AB}{AC}$;
(2)过点A作AP⊥BC,垂足为P,根据三角形的面积计算公式,得出$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{BD}{CD}$;
(3)根据(1)、(2)的结论,即可得出结论.
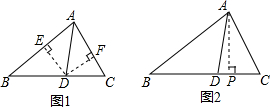
解答  解:(1)如图1,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
解:(1)如图1,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
∵AD平分∠BAC,
∴DE=DF,
又∵S△ABD=$\frac{1}{2}$×AB×DE,S△ACD=$\frac{1}{2}$×AC×DF,
∴$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{AB}{AC}$,
故答案为:DE,DF,AB,DE,AC,DF;
(2)如图2,过点A作AP⊥BC,垂足为P,
∵S△ABD=$\frac{1}{2}$×BD×AP,S△ACD=$\frac{1}{2}$×CD×AP,
∴则$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{BD}{CD}$,
故答案为:$\frac{1}{2}$×BD×AP,$\frac{1}{2}$×CD×AP;
(3)根据(1)、(2)的结论,可得:
若在△ABC中,AD平分∠BAC,则线段AB、AC、BD、CD的关系为:$\frac{AB}{AC}$=$\frac{BD}{CD}$.
故答案为:$\frac{AB}{AC}$=$\frac{BD}{CD}$.
点评 本题主要考查了角平分线的性质以及三角形的面积的计算公式的运用,解决问题的关键是掌握:角的平分线上的点到角的两边的距离相等.解题时注意:等高的三角形的面积之比等于底边之比.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{k}{x}$-1(k≠0) | B. | y=k(x-1)(k≠0) | C. | y=$\frac{k}{x-1}$(k≠0) | D. | y=$\frac{x-1}{k}$(k≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:
某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
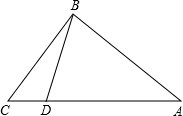 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
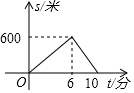 小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )
小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
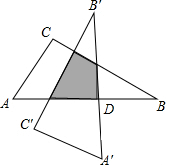 如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2<y3<y1 | D. | y3<y2<y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com