
����Ŀ����ͼ��������y=��x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����ߵĶԳ���DE��x���ڵ�E������BD��
��1����A��B��C����������ߵĺ�������ʽ��
��2����P���߶�BD��һ�㣬��PE=PCʱ�����P�����ꣻ
��3���ڣ�2���������£�����P��PF��x���ڵ�F��GΪ��������һ���㣬MΪx����һ���㣬NΪֱ��PF��һ���㣬����F��M��N��GΪ������ı�����������ʱ���������M�����꣮
���𰸡�
��1��
�⣺��������y=��x2+bx+c����A����1��0����B��3��0�����㣬
�� ![]() ����ã�
����ã� ![]() ��
��
�ྭ��A��B��C����������ߵĺ�������ʽΪy=��x2+2x+3��
��2��
�⣺��ͼ1������PC��PE��

x=�� ![]() =��
=�� ![]() =1��
=1��
��x=1ʱ��y=4��
���D��������1��4����
��ֱ��BD�Ľ���ʽΪ��y=mx+n��
�� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��BD�Ľ���ʽΪy=��2x+6��
���P��������x����2x+6����
��PC2=x2+��3+2x��6��2��PE2=��x��1��2+����2x+6��2��
��PC=PE��
��x2+��3+2x��6��2=��x��1��2+����2x+6��2��
��ã�x=2��
��y=��2��2+6=2��
���P��������2��2����
��3��
�⣺���M������Ϊ��a��0�������G������Ϊ��a����a2+2a+3����
����F��M��N��GΪ������ı����������Σ�
��FM=MG����|2��a|=|��a2+2a+3|��
��2��a=��a2+2a+3ʱ��
�����ã�a2��3a��1=0��
��ã�a= ![]() ��
��
��2��a=������a2+2a+3��ʱ��
�����ã�a2��a��5=0��
��ã�a= ![]() ��
��
�൱��F��M��N��GΪ������ı�����������ʱ����M������Ϊ�� ![]() ��0������
��0������ ![]() ��0������
��0������ ![]() ��0������
��0������ ![]() ��0����
��0����
����������1�����ô���ϵ���������A��B��C����������ߵĺ�������ʽ����2������PC��PE�����ù�ʽ�������D�����꣬���ô���ϵ�������ֱ��BD�Ľ���ʽ�������P������Ϊ��x����2x+6�������ù��ɶ�����ʾ��PC2��PE2 �� ���������г����̣��ⷽ�����x��ֵ�����������P�����ꣻ��3�����M������Ϊ��a��0������ʾ����G�����꣬���������ε������г����̣��ⷽ�̼��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��Բ��ֽƬ����ͼ��ʾ��ʽ�۵����κ�չ����ͼ�е����߱�ʾ�ۺۣ��� ![]() �Ķ����ǣ� ��
�Ķ����ǣ� �� 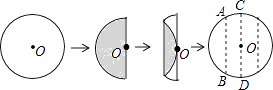
A.120��
B.135��
C.150��
D.165��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺����1��2017��4cos60��+ ![]() +
+ ![]()
��2���Ȼ�������ֵ����a�� ![]() ����
���� ![]() ������a����a2+3a��1=0��
������a����a2+3a��1=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺|1�� ![]() |+3tan30�㩁��2017���У�0������
|+3tan30�㩁��2017���У�0������ ![]() ����1 ��
����1 ��
��2����֪x��y���㷽���� ![]() �������ʽ
�������ʽ ![]()
![]() ��
�� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���CAB=30�㣬��C=90�㣮AD= ![]() AC��AB=8��E��AB������һ�㣬F��AC������һ�㣬������DEFB����̳���Ϊ ��
AC��AB=8��E��AB������һ�㣬F��AC������һ�㣬������DEFB����̳���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ����Rt��ABC��AC��Ϊֱ������O��б��AB�ڵ�E������EO���ӳ���BC���ӳ����ڵ�D����FΪBC���е㣬����EF�� 
��1����֤��EF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ3����EAC=60�㣬��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�E����DAB=��CDB=90�㣬��ABD=45�㣬��DCA=30�㣬AB=6����AE= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ�DGƽ�֡�ADB��AB�ڵ�G��GF��BD��F�� 
��1����֤����ADG�ա�FDG��
��2����BG=2AG��BD=2 ![]() ����AD�ij���
����AD�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com