
【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.
(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程)
【答案】
(1)解:∵CD∥OA,
∴∠BCD=∠O,
∵∠O=∠ADC,
∴∠BCD=∠CDA,
∴AD∥OB;
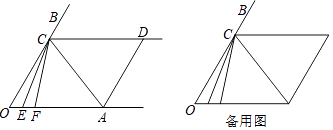
(2)解:∵∠O=∠ADC=60°,
∴∠BCD=60°,
∴∠OCD=120°,
∵CD∥OA,
∴∠DCA=∠CAO,
∵∠FCA=∠FAC,
∴∠DCA=FCA,
∵CE平分∠OCF,
∴∠OCE=∠FCE,
∴∠ECF+∠ACF= ![]() ∠OCD=60°,
∠OCD=60°,
∴∠ACE=60°;
(3)解:∠CAD+∠OEC=180°,
理由:∵AD∥OC,
∴∠CAD=∠OCA,
∵∠OCA=∠OCE+∠ACE=60°+∠OCE,
∵∠AEC=∠O+∠OCE=60°+∠OCE,
∴∠AEC=∠CAD,
∵∠AEC+∠OEC=180°,
∴∠CAD+∠OEC=180°.
【解析】(1)首先根据平行线的性质得到∠BCD=∠O,然后通过等量代换得到∠BCD=∠CDA,于是得到结论;
(2)首先依据邻补角的定义得到∠OCD=120°,然后再根据平行线的性质得到∠DCA=∠CAO,通过等量代换得到∠DCA=FCA,由角平分线的定义得到∠OCE=∠FCE,于是得到结论;
(3)首先根据平行线的性质得到∠CAD=∠OCA,然后可推出∠AEC=∠CAD,接下来,根据平角的定义得到∠AEC+∠OEC=180°,于是得到结论.
【考点精析】根据题目的已知条件,利用平行线的性质和平移的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.


科目:初中数学 来源: 题型:
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.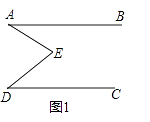
(1)探究猜想:
①若∠A=35°,∠D=30°,则∠AED等于多少度?
②若∠A=48°,∠D=32°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线EF与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求写出证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.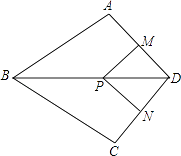
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.﹣2x2y3xy2=﹣6x2y2
B.(﹣x﹣2y)(x+2y)=x2﹣4y2
C.6x3y2÷2x2y=3xy
D.(4x3y2)2=16x9y4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号) 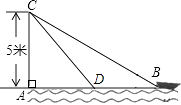
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
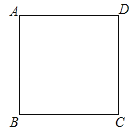
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com