
分析 由关于x的方程(a+2)x2-2ax+a=0有两个不相等的实数根,根据一元二次方程的二次项系数不为0和根的判别式求出a的取值范围.设抛物线y=x2-(2a+1)x+2a-5与x轴的两个交点坐标分别为(α,0)、(β,0),且α<β,得出α、β是关于x的方程x2-(2a+1)x+2a-5=0的两个不相等的实数根,由抛物线y=x2-(2a+1)x+2a-5与x轴的两个交点分别位于点(2,0)的两旁,利用根与系数的关系确定a的取值范围;把|x1|+|x2|=2$\sqrt{2}$变形后,利用根与系数的关系求出a的值.
解答 解:∵关于x的方程(a+2)x2-2ax+a=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{a+2≠0}\\{△=(-2a)^{2}-4a(a+2)>0}\end{array}\right.$,
解得:a<0,且a≠-2 ①
设抛物线y=x2-(2a+1)x+2a-5与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,
则α、β是关于x的方程x2-(2a+1)x+2a-5=0的两个不相等的实数根,
∵△=[-(2a+1)]2-4×1×(2a-5)=(2a-1)2+21>0,
∴a为任意实数②
由根与系数关系得:α+β=2a+1,αβ=2a-5.
∵抛物线y=x2-(2a+1)x+2a-5与x轴的两个交点分别位于点(2,0)的两旁,
∴α<2,β>2,
∴(α-2)(β-2)<0,
∴αβ-2(α+β)+4<0,
∴2a-5-2(2a+1)+4<0
解得:a>-$\frac{3}{2}$③
由①、②、③得a的取值范围是-$\frac{3}{2}$<a<0;
∵x1和x2是关于x的方程(a+2)x2-2ax+a=0的两个不相等的实数根
∴x1+x2=$\frac{2a}{a+2}$,x1x2=$\frac{a}{a+2}$,
∵-$\frac{3}{2}$<a<0,
∴a+2>0,
∴x1x2=$\frac{a}{a+2}$<0.
不妨设x1>0,x2<0,
∴|x1|+|x2|=x1-x2=2$\sqrt{2}$,
∴x12-2x1x2+x22=8,即(x1+x2)2-4x1x2=8,
∴($\frac{2a}{a+2}$)2-$\frac{4a}{a+2}$=8,
解这个方程,得:a1=-4,a2=-1,
经检验,a1=-4,a2=-1都是方程($\frac{2a}{a+2}$)2-$\frac{4a}{a+2}$=8的根.
∵a=-4<-$\frac{3}{2}$,舍去,
∴a=-1为所求.
故答案为-1.
点评 本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,一元二次方程根的判别式以及根与系数的关系,代数式变形等知识,综合性较强.利用根的判别式以及根与系数的关系求出-$\frac{3}{2}$<a<0是解题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:解答题
 某化妆公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):
某化妆公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):查看答案和解析>>
科目:初中数学 来源: 题型:填空题
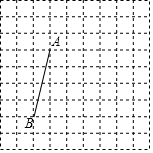 如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.
如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
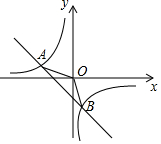 如图,一次函数y=ax+b(a,b为常数,并且a≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交相交于点A(-2,1),B(1,n)
如图,一次函数y=ax+b(a,b为常数,并且a≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交相交于点A(-2,1),B(1,n)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+a3=a5 | B. | (a3)2÷a6=1 | C. | a2•a3=a6 | D. | ($\sqrt{2}$+$\sqrt{3}$)2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
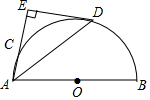 如图,AB是半圆O的直径,且AB=4,点C是半圆上一点,半圆的切线DE垂直直线AC于点E.
如图,AB是半圆O的直径,且AB=4,点C是半圆上一点,半圆的切线DE垂直直线AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com