练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，等边三角形ABC中，点D，E分别为AB，AC的中点，则∠DEC的度数为（　　）
    A．150°B．120°C．60°D．30°

    分析 根据等边三角形的性质，可得∠C的度数，根据三角形中位线的性质，可得DE与BC的关系，根据平行线的性质，可得答案．

    解答 解：∵△ABC是等边三角形，
    ∴∠C=60°，
    ∵点D、E分别为边AB、AC的中点，
    ∴DE∥BC，
    ∴∠DEC=180°-∠C=180°-60°=120°，
    故选：B．

    点评 本题考查了三角形中位线定理以及等边三角形的性质，解题的关键是掌握三角形的中位线平行于第三边且等于第三边的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．（1）|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$．
    （2）$\sqrt{（-5）^{2}}$+（$\sqrt{3}$）2-$\root{3}{27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

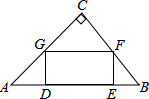    7．如图，在直角三角形ABC中，∠C=90°，矩形DEFG的四个顶点都在△ABC的边上，已知：AC=8，BC=6．
    （1）当四边形DEFG为正方形时，求EF的长；
    （2）△BEF与△FCG能全等吗？若能，请你求出EF的长；若不能，请说明理由；
    （3）△BEF与△ADG能全等吗？若能，请你求出EF的长；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

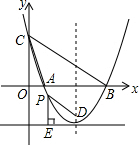    4．已知抛物线y=$\frac{1}{2}$x2+2（m+1）x-m+1与x轴交于点A、B，与y轴交于点C，其对称轴是直线x=4．
    （1）求抛物线的解析式是顶点坐标；
    （2）求C点的坐标及△ABC的面积；
    （3）已知与x轴平行的直线y=t及抛物线对称轴上的点D（4，t+1），问是否存在这样的t值，使得抛物线上任意一点P（a，b）到这条直线的距离等于P点到D点的距离？若存在，则请求出t的值；若不存在，则说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示，将纸片△ABC沿DE折叠，点A落在点A′处，已知∠1=140°，∠2=40°，求∠A的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

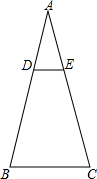    1．如图，在△ABC中，DE∥BC，且$\frac{AE}{EC}$=$\frac{1}{2}$，则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=（　　）
    A．1：4B．1：9C．3：4D．8：9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

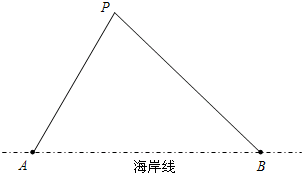    8．捍卫祖国海疆是人民海军的神圣职责．我海军在相距20海里的A、B两地设立观测站（海岸线是过A、B的直线）．按国际惯例，海岸线以外12海里范围内均为我国领海，外国船只除特许外，不得私自进入我国领海．某日，观测员发现一外国船只行驶至P处，在A观测站测得∠BAP=63°，同时在B观测站测得∠ABP=34°．问此时是否需要向此未经特许的船只发出警告，命令其退出我国领海？（参考数据：sin63°≈$\frac{9}{10}$，tan63°≈2，sin34°≈$\frac{3}{5}$，tan34°≈$\frac{2}{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若$\sqrt{{a}^{2}}$=-a成立，则满足的条件是（　　）
    A．a＞0B．a＜0C．a≥0D．a≤0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列运算正确的是（　　）
    A．a3•a2=a5B．（-a2）3=a6C．（ab）3=ab3D．a8÷a2=a4

    查看答案和解析>>

    同步练习册答案