
 有一石拱桥的桥拱是圆弧形,如下图所示,正常水位下水面宽AB=60米,水面到拱顶距离CD=18米,当洪水泛滥,水面宽MN=32米时是否需要采取紧急措施?请说明理由(当水面距拱顶3米以内时需采取紧急措施).
有一石拱桥的桥拱是圆弧形,如下图所示,正常水位下水面宽AB=60米,水面到拱顶距离CD=18米,当洪水泛滥,水面宽MN=32米时是否需要采取紧急措施?请说明理由(当水面距拱顶3米以内时需采取紧急措施). 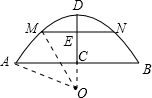 解:不需要采取紧急措施.
解:不需要采取紧急措施.| OM2-ME2 |
| 342-162 |


科目:初中数学 来源: 题型:
 24、有一石拱桥的桥拱是圆弧形,如下图所示,正常水位下水面宽AB=60m,水面到拱项距离CD=18m,当洪水泛滥时,水面宽MN=32m时,高度为5m的船是否能通过该桥?请说明理由.
24、有一石拱桥的桥拱是圆弧形,如下图所示,正常水位下水面宽AB=60m,水面到拱项距离CD=18m,当洪水泛滥时,水面宽MN=32m时,高度为5m的船是否能通过该桥?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 25、有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面到拱顶距离为3.5米时需要采取紧急措施,当水面宽MN=32m时是否需要采取紧急措施?请说明理由.
25、有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面到拱顶距离为3.5米时需要采取紧急措施,当水面宽MN=32m时是否需要采取紧急措施?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
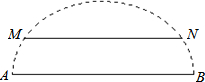 应用题:有一石拱桥的桥拱是圆弧形,当水面到拱顶的距离小于3.5米时,需要采取紧急措施.如图所示,正常水位下水面宽AB=60米,水面到拱顶的距离18米.
应用题:有一石拱桥的桥拱是圆弧形,当水面到拱顶的距离小于3.5米时,需要采取紧急措施.如图所示,正常水位下水面宽AB=60米,水面到拱顶的距离18米.查看答案和解析>>
科目:初中数学 来源:2010-2011学年江西省赣州市寻乌中学九年级(上)第一次月考数学试卷(21-24章)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com