
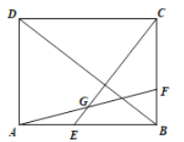
【题目】如图,在矩形![]() 中,
中,![]() 为对角线,过点
为对角线,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则线段
,则线段![]() 的长为______.
的长为______.
【答案】![]()
【解析】
连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.利用全等三角形的性质证明OC=CM,∠ACG=∠GCM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,可得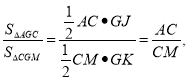
 推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
解:连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.

∵四边形ABCD是矩形, ∴OA=OC,
∵AG=GF=CF, ∴∠FCG=∠FGC,OG∥CF,
∴∠OGC=∠FCG=∠FGC,
∵CE⊥BD, ∴∠GNO=∠GNM=90°,
∵GN=GN, ∴△GNO≌△GNM(ASA),
∴ON=NM,OG=GM,
∵∠CNO=∠CNM=90°,CN=CN,
∴△CNO≌△CNM(SAS),
∴∠OCN=∠MCN,OC=MC= ![]() AC,
AC,
∴GC平分∠ACM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,
∴ 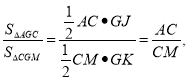
同理:
![]()
∴AG=2GM,
∵AG=GF, ∴GM=MF,
∵∠MOG=∠MBF,∠OMG=∠BMF,
∴△MOG≌△MBF(AAS),
∴OG=BF=GM=FM,
设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,
∴BC=3k,
在Rt△ABF中,∵![]() ∴
∴![]() ①,
①,
在Rt△ABC中,∵![]() AC=BD=
AC=BD= ![]()
∴![]() ②,
②,
由①②可得AB=![]()
故答案为![]()


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C、D的坐标及四边形ABDC的面积;
(2)若点Q在线的CD上移动(不包括C,D两点).QO与线段AB,CD所成的角∠1与∠2如图所示,给出下列两个结论:①∠1+∠2的值不变;②![]() 的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
(3)在y轴正半轴上是否存在点P,使得S△CDP=S△PBO?如果有,试求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
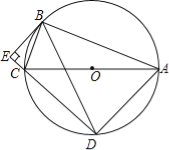
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
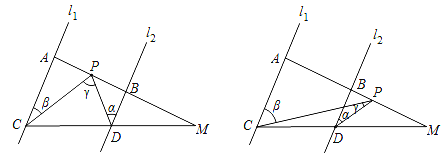
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③ 2a+b=0;④b2-4ac>0 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有()

A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季是垂钓的好季节.一天甲、乙两人到松花江的![]() 处钓鱼,突然发现在
处钓鱼,突然发现在![]() 处有一人不慎落入江中呼喊救命.如图,在
处有一人不慎落入江中呼喊救命.如图,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从
方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从![]() 处跳水游向
处跳水游向![]() 处救人;此时乙从
处救人;此时乙从![]() 沿岸边往正东方向奔跑40米到达
沿岸边往正东方向奔跑40米到达![]() 处,再从
处,再从![]() 处下水游向
处下水游向![]() 处救人,已知
处救人,已知![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
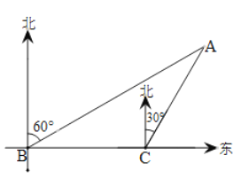
(1)求![]() 、
、![]() 的长.
的长.
(2)试问甲、乙二人谁能先救到人,请通过计算说明理由.(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
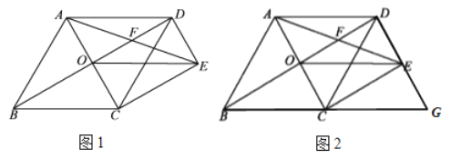
(1)求证:![]() ;
;
(2)如图2,延长![]() 和
和![]() 相交于点
相交于点![]() ,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形
,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形![]() 和四边形
和四边形![]() 外)
外)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将1、![]() 、
、![]() 三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(9,3)与(2019,2019)表示的两个数的积是( )
三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(9,3)与(2019,2019)表示的两个数的积是( )

A.1B.2C.3D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com