
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
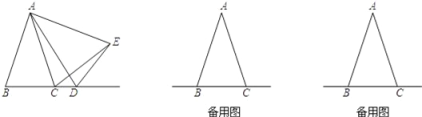
【答案】(1)30°;(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β;②当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.
【解析】
(1)证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;
(2)①证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②分D在线段BC上时和当点D在线段BC延长线或反向延长线上时两种情况求解即可.
(1)解:(1)∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
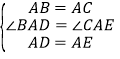 ,
,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=30°,
∴∠DCE=30°.
故答案为30;;
(2)①解:当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,
理由是:
∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中
∵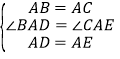 ,
,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
②解:当D在线段BC上时,α+β=180°,
理由如下:
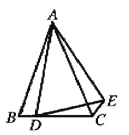
∵∠BAC=∠DAE,
∴∠BAD=∠CAE;
在△BAD与△CAE中,
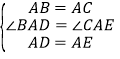 ,
,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∴β=∠ABC+∠ACB,
∵∠ABC+∠ACB=180°-α,
∴α+β=180°.
故答案为α+β=180°;
当点D在线段BC延长线或反向延长线上时,α=β,证明如①.
∴当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.


科目:初中数学 来源: 题型:
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年8月第29届奥运会将在北京开幕,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2008年8月8日20时应是( )
![]()
A. 伦敦时间2008年8月8日11时
B. 巴黎时间2008年8月8日13时
C. 纽约时间2008年8月8日5时
D. 汉城时间2008年8月8日19时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.

(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
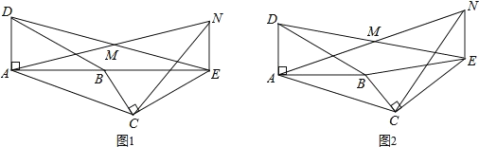
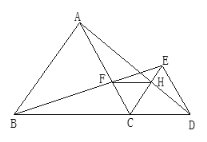
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
(1)求证:△BCE≌△ACD;
(2)求证:FC=HC
(3)求证:FH∥BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
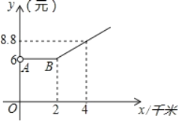
【题目】某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示.
(1)图中AB段的意义是 .
(2)当x>2时,y与x的函数关系式为 .
(3)张先生打算乘出租车从甲地去丙地,但需途径乙地办点事,已知甲地到乙地的路程为1km,乙地至丙地的路程超过3km,现有两种打车方案:
方案一:先打车从甲地到乙地,办完事后,再打另一部出租车去丙地;
方案二:先打车从甲地到乙地,让出租车司机等候,办完事后,继续乘该车去丙地(出租车等候期间,张先生每分钟另付0.2元,假设计价器不变).
张先生应选择哪种方案较为合算?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com