
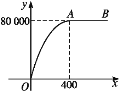
【题目】某厂家生产一种产品,月初需要一次性投资25 000元,每生产一件产品需增加投入100元.设x(件)是月生产量,y(元)是销售完x件产品所得的总销售额,y与x的关系如图中的图象所示,图象中从点O到点A的部分是抛物线的一部分,且点A是抛物线的顶点,点A后面的部分与x轴平行.
(1)求y关于x的函数关系式;
(2)设月纯利润为z,求z关于x的函数关系式;
(3)当月产量为多少件时,厂家所获利润最大?最大利润为多少元?
【答案】(1)y=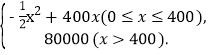 (2)z=
(2)z= ;(3) 当月产量为300台时,利润最大,最大利润为20 000元
;(3) 当月产量为300台时,利润最大,最大利润为20 000元
【解析】
(1)根据顶点坐标设二次函数的解析式为y=a(x-400)2+80000,把O(0,0)代入可求出a的值,即可得![]() 时y关于x的函数关系式,由点A后面的部分与x轴平行可得x>400时y关于x的函数关系式;(2)根据月纯利润=总销售额-月初投资-产品成本即可得出答案;(3)分别计算x>400时和
时y关于x的函数关系式,由点A后面的部分与x轴平行可得x>400时y关于x的函数关系式;(2)根据月纯利润=总销售额-月初投资-产品成本即可得出答案;(3)分别计算x>400时和![]() 时利润的最大值即可.
时利润的最大值即可.
(1)当![]() 时,设函数解析式为y=a(x-400)2+80000,
时,设函数解析式为y=a(x-400)2+80000,
∵图像经过O(0,0),
∴a(x-400)2+80000=0,
解得:a=-![]() ,
,
∴![]() 时y关于x的函数关系式为y=-
时y关于x的函数关系式为y=-![]() (x-400)2+80000=-
(x-400)2+80000=-![]() x2+400x.
x2+400x.
∵当x>400时,点A后面的部分与x轴平行,
∴x>400时y关于x的函数关系式为y=80000.
∴y关于x的函数关系式为:y=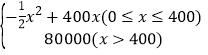 .
.
(2)∵月纯利润=总销售额-月初投资-产品成本,
∴z=y-25000-100x,
当0≤x≤400时,z=-![]() x2+400x-25000-100x=-
x2+400x-25000-100x=-![]() x2+300x-25000,
x2+300x-25000,
当x>400时,z=80000-25000-100x=-100x+55000,
∴z关于x的函数关系式为z=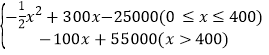
(3)当x>400时,z<-100×400+55000=15000(元);
当0≤x≤400时,z=-![]() x2+300x-25000=-
x2+300x-25000=-![]() (x-300)2+20000.
(x-300)2+20000.
所以,当x=300时,z最大=20000(元).
答:当月产量为300台时,利润最大,最大利润为20000元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
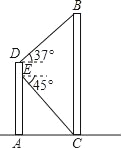
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
查看答案和解析>>
科目:初中数学 来源: 题型:
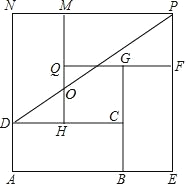
【题目】如图,已知长方形 ABCD 中,AB=a,BC=b.正方形 AEPN 是由长方形 ABCD经过图形的运动形成的.其中长方形 GBEF 是由长方形 ABCD 绕着 B 点顺时针旋转 90° 得到的,长方形 HMND 是由将长方形 ABCD 绕着 D 点逆时针旋转 90°得到的,长方形QFPM 是长方形 ABCD 经过平移得到的.
(1) 长方形 QFPM 是由长方形 ABCD 经过怎样平移得到的?
(2) 用含 a、b 的代数式分别表示正方形 HCGQ 的面积;
(3) 连接 DP,交 HM 于点 O.用 a、b 的代数式分别表示 OM.
查看答案和解析>>
科目:初中数学 来源: 题型:
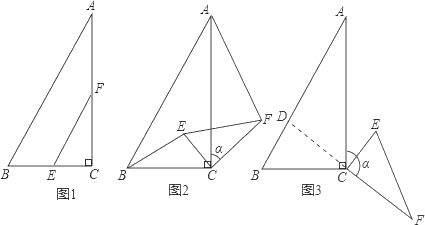
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,![]() = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
(3)当每斤的售价定为多少元时,每天获利最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工材料经销公司购进一种化工原料若干千克,物价部门规定其销售单价不低于进价,不高于60元/千克,经市场调查发现:销售单价定为60元/千克时,每日销售20千克;如调整价格,每降价1元/千克,每日可多销售2千克.
(1)已知某天售出该化工原料40千克,则当天的销售单价为 元/千克;
(2)该公司现有员工2名,每天支付员工的工资为每人每天90元,每天应支付其他费用108元,当某天的销售价为46元/千克时,收支恰好平衡.
①求这种化工原料的进价;
②若公司每天的纯利润(收入﹣支出)全部用来偿还一笔10000元的借款,则至少需多少天才能还清借款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2007年上海国际汽车展期间,某公司对参观本次车展盛会的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中:
①将消费者年收入的情况整理后,制成表格如下:
年收入(万元) | 4.8 | 6 | 7.2 | 9 | 10 |
被调查的消费者人数(人) | 150 | 338 | 160 | 60 | 42 |
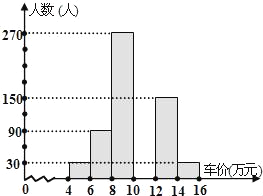
②将消费者打算购买小车的情况整理后,绘制出频数分布直方图(如图,尚未绘完整).(注:每组包含最小值不包含最大值.)请你根据以上信息,回答下列问题:
(1)根据①中信息可知,被调查消费者的年收入的中位数是______万元.
(2)请在图中补全这个频数分布直方图.
(3)打算购买价格10万元以下(不含10万元)小车的消费者人数占被调查消费者人数的百分比是_______.
(4)本次调查的结果,是否能够代表全市所有居民的年收入情况和购车意向?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉素有“首义之区”的美名,2011年9月9日,武汉与台湾将共同纪念辛亥革命一百周年.某校为了了解全校学生对辛亥革命的了解程度,随机抽取了部分学生进行问卷调查,并根据收集的信息进行了统计,绘制了下面尚不完整的统计图. 根据以上的信息,下列判断:①参加问卷调查的学生有50名;②参加进行问卷调查的学生中,“基本了解”的有10人;③扇形图中“基本了解”部分的扇形的圆心角的度数是108°;④在参加进行问卷调查的学生中,“了解”的学生占10%.
其中结论正确的序号是( ).
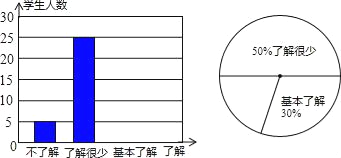
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com