
【题目】如图所示,在平行四边形ABCD中,AD∥BC,过B作BE⊥AD交AD于点E,AB=13cm,BC=21cm,AE=5cm.动点P从点C出发,在线段CB上以每秒1cm的速度向点B运动,动点Q同时从点A出发,在线段AD上以每秒2cm的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动,设运动的时间为t(秒)
(1)当t为何值时,四边形PCDQ是平行四边形?
(2)当t为何值时,△QDP的面积为60cm2?
(3)当t为何值时,PD=PQ?

【答案】(1)当t=7时,四边形PCDQ是平行四边形;(2)当t=![]() 时,△QDP的面积为60cm2;(3)当t=
时,△QDP的面积为60cm2;(3)当t=![]() 时,PD=PQ.
时,PD=PQ.
【解析】
(1)根据题意用t表示出CP=t,AQ=2t,根据平行四边形的判定定理列出方程,解方程即可;
(2)根据三角形的面积公式列方程,解方程得到答案;
(3)根据等腰三角形的三线合一得到DH=![]() DQ,列方程计算即可.
DQ,列方程计算即可.
(1)由题意得,CP=t,AQ=2t,
∴QD=21﹣2t,
∵AD∥BC,
∴当DQ=PC时,四边形PCDQ是平行四边形,
则21﹣2t=t,
解得,t=7,
∴当t=7时,四边形PCDQ是平行四边形;
(2)在Rt△ABE中,BE=![]() =12,
=12,
由题意得,![]() ×(21﹣2t)×12=60,
×(21﹣2t)×12=60,
解得,t=![]() ,
,
∴当t=![]() 时,△QDP的面积为60cm2;
时,△QDP的面积为60cm2;
(3)作PH⊥DQ于H,DG⊥BC于G,则四边形HPGD为矩形,

∴PG=HD,
由题意得,CG=AE=5,
∴PG=t﹣5,
当PD=PQ,PH⊥DQ时,DH=![]() DQ,即t﹣5=
DQ,即t﹣5=![]() (21﹣2t),
(21﹣2t),
解得,t=![]() ,
,
则当t=![]() 时,PD=PQ.
时,PD=PQ.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,射线 OC在∠AOB的内部,图中共有 3个角:∠AOB、∠AOC 和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线 OC是∠AOB的奇妙线.
(1)一个角的角平分线_______这个角的奇妙线.(填是或不是);
(2)如图 2,若∠MPN=60°,射线 PQ绕点 P从 PN位置开始,以每秒 10°的速度逆时针旋转,当∠QPN首次等于 180°时停止旋转,设旋转的时间为 t(s).
① 当 t为何值时,射线 PM是∠QPN 的奇妙线?

②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转,并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从A地出发前往B地,甲先出发1分钟后,乙再出发,乙出发一段时间后返回A地取物品,甲、乙两人同时达到B地和A地,并立即掉头相向而行直至相遇,甲、乙两人之间相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则甲、乙两人最后相遇时,乙距B地的路程是_____米.
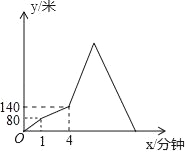
查看答案和解析>>
科目:初中数学 来源: 题型:
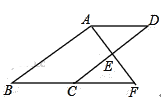
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB⊥AF,BC=12,EF=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
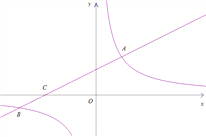
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线![]() 的解析式;
的解析式;
(2)若点P在x轴上,且![]() ,求点P的坐 标(直接写出结果).
,求点P的坐 标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,直线a与直线b交于点O,△ABC的顶点均在格点上.
(1)△ABC向右平移 个单位长度到△A1B1C1位置;
(2)对△ABC分别作下列变换:
① 画出△ABC关于直线a对称的△A2B2C2;
② 将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △ 与△ 成轴对称,对称轴是直线 ;
② △ 与△ 成中心对称,并在图中标出对称中心D的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
材料1:对称,也许是中国人最喜欢的。建筑师梁思成曾说过:“无论东方、西方,再没有一个民族对中轴对称线如此钟爱与恪守。”放眼中国的建筑,无论是宫殿、庙宇、亭台、楼阁、园林无不有着对称之美。数学世界也里有一些正整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:11、101、2332、1234321、…,像这样的数我们叫它“对称数”.
材料2:如果一个三位数![]() ,满足a+b+c=8,我们就称这个三位数为“发财数”.
,满足a+b+c=8,我们就称这个三位数为“发财数”.
(1)请直接写出既是“对称数”又是“发财数”的所有三位数;
(2)一个三位“对称数”十位数字为7,它的各数位上的数字之和是一个自然数的平方,求这个三位数(请写出必要的推理过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
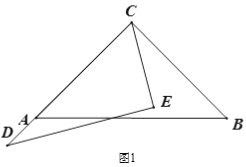
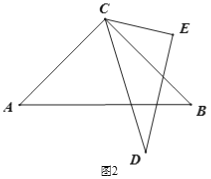
【题目】已知将一副三角板(直角三角板ABC和直角三角板CDE,∠ACB=90°,∠ECD=60°)如图1摆放,点D、A、C在一条直线上,将直角三角板CDE绕点C逆时针方向转动,变化摆放如图位置.
(1) 如图2,当∠ACD为多少度时,CB恰好平分∠ECD?
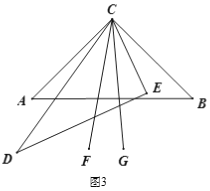
(2) 如图3,当三角板CDE摆放在∠ACB内部时,作射线CF平分∠ACE,射线CG平分∠BCD,如果三角形CDE在∠ACB内绕点C任意转动,∠FCG的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
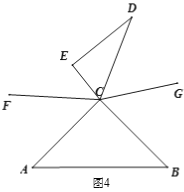
(3) 如图4,当三角板CDE转到∠ACB外部时,射线CF、CG仍然分别平分∠ACE、∠BCD,在旋转过程中,(2)中的结论是否成立?如果结论成立,请说明理由;如果不成立,请写出你的结论并根据图4说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com