练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

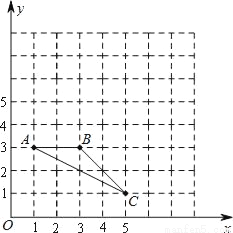
    已知△ABC在平面直角坐标系中的位置如图所示．

    （1）分别写出图中点A和点C的坐标；

    （2）画出△ABC绕点A按逆时针方向旋转90°后的△AB′C′；

    （3）在（2）的条件下，求点C旋转到点C′所经过的路线长（结果保留π）．

    （1）点A坐标为（1，3）；点C坐标为（5，1）；（2）图形见解析（3）π 【解析】试题分析：（1）根据直角坐标系的特点写出各点的坐标； （2）分别将点绕点按逆时针方向旋转90°后得到点，然后顺次连接； （3）点旋转到点的轨迹为圆弧，根据弧长公式和扇形的面积求解． 试题解析： （2）所作图形如图所示： （3） ∴点旋转到点所经过的路线长 则线段旋转到新位置是...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第25章 概率初步 单元测试卷 题型：解答题

    在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个．

    (1)先从袋子中取出m(m>1)个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A．请完成下列表格：

    事件A

    必然事件

    随机事件

    m的值

    (2)先从袋子中取出m个红球，再放入m个一样的黑球并摇匀，随机摸出1个球是黑球的可能性大小是，求m的值．

    (1)填表见解析；（2）2. 【解析】试题分析：（1）当袋子中全部为黑球时，摸出黑球才是必然事件，否则就是随机事件； （2）利用概率公式列出方程，求得m的值即可． 试题解析：（1）当袋子中全为黑球，即摸出4个红球时，摸到黑球是必然事件； 当摸出2个或3个时，摸到黑球为随机事件， 故答案为：4；2，3. （2）根据题意得： ， 解得：m=2， 所以m的...

    查看答案和解析>>

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：单选题

    已知点P(3,-2)与点Q关于x轴对称，则Q点的坐标为( )

    A. (-3,2) B. (-3,-2) C. (2,3) D. (3,2)

    D 【解析】试题解析：根据轴对称的性质，得点P（3，-2）关于x轴对称的点的坐标为（3，2）． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

    如图，铁路道口的栏杆短臂长1m，长臂长16m.当短臂端点下降0.5m时，长臂端点升高（杆的宽度忽略不计）

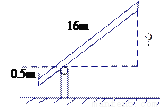
    A. 4m B. 6m C. 8m D. 12m

    C 【解析】试题分析：设长臂端点升高x米，则，∴解得：x=8．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

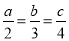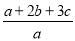    若，则等于（　　）

    A. 8 B. 9 C. 10 D. 11

    C 【解析】试题解析：设， 则a=2k，b=3k，c=4k， 即， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：填空题

    如图，AC是⊙O的直径，∠ACB=60°，连接AB，过A、B两点分别作⊙O的切线，两切线交于点P．若已知⊙O的半径为1，则△PAB的周长为_____．

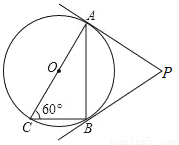
    【解析】根据圆周角定理的推论及切线长定理，即可得出答案 【解析】 ∵AC是⊙O的直径， ∴∠ABC=90°， ∵∠ACB=60°， ∴∠BAC=30°， ∴CB=1，AB=， ∵AP为切线， ∴∠CAP=90°， ∴∠PAB=60°， 又∵AP=BP， ∴△PAB为正三角形， ∴△PAB的周长为3．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：单选题

    已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有（　　）

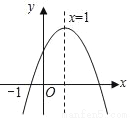
    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】试题分析：开口向下，则a＜0，对称轴在y轴右边，则b＞0，与y轴交于正半轴，则c＞0，∴abc＜0，∴①正确；当x=－1时，y＜0，即a－b+c＜0，∴b＞a+c，∴②正确；因为对称轴为1，即－=1，则 2a=－b，∴2a+b=0，∴③错误；∵图象与x轴有两个交点，则－4ac＞0，∴④错误．

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型：填空题

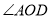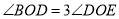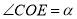    如图，已知为直线上一点， 平分， ， ，则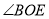的度数为_________．（用含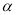的代数式表示）

    【解析】【解析】 设为，∴． ∵平分，∴， ∴， ∴． 故答案为：360°-4α．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第3章 整式及其加减 单元测试卷 题型：解答题

    若代数式(4x2－mx－3y＋4)－(8nx2－x＋2y－3)的值与字母x的取值无关，求代数式(－m2＋2mn－n2)－2(mn－3m2)＋3(2n2－mn)的值．

    . 【解析】试题分析：已知代数式去括号合并后，根据结果与x的取值无关，求出m与n的值，原式去括号合并后代入数值进行计算即可求出代数式的值. 试题解析：(4x2－mx－3y＋4)－(8nx2－x＋2y－3) ＝4x2－mx－3y＋4－8nx2＋x－2y＋3 ＝(4－8n)x2＋(1－m)x－5y＋7， ∵上式的值与字母x的取值无关， ∴4－8n＝0，1－m＝0，即...

    查看答案和解析>>

    同步练习册答案