
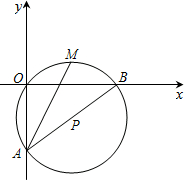
 如图在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上,M为劣弧OB的中点.
如图在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上,M为劣弧OB的中点.分析 (1)如图1中,过点P作PH⊥OB于点H,根据垂径定理,三角形的中位线定理即可解决问题.
(2)根据等弧所对的圆周角相等即可证明.
(3)如图2中,连接PM,易知PM⊥OB于H,只要证明AN=AB,可得点N坐标,求出OH、MH即可得M坐标.
解答 解:(1)如图1中,过点P作PH⊥OB于点H.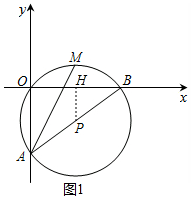
∵O(0,0),A(0,-6),B(8,0),
∴OB=8,OA=6,
又∵OA⊥OB,
∴AB=10,
∴∠AOB=90°,
∴AB为⊙P的直径,
∴⊙P的半径为5,
∵PH⊥OB,PH过圆心O,
∴H为OB的中点,
又∵P为AB的中点,
∴PH=$\frac{1}{2}$OA=3,OH=$\frac{1}{2}$OB=4,
∴P的坐标为(4,-3).
(2)∵M为劣弧OB的中点,
∴$\widehat{OM}$=$\widehat{BM}$,
∴∠OAM=∠BAM,
∴AM是∠OAB的角平分线.
(3)如图2中,连接PM,易知PM⊥OB于H,
由(1)知,AB 为⊙P的直径,
∴∠AMB=90°,
∴AM⊥BM,
由(2)知,AM是∠OAB的角平分线,
∴∠ABM=∠ANM,
∴AB=AN=10,
∴ON=4,
∴N的坐标为:(0,4),
由(1)知,PH=3,
∴MH=2,
∴M的坐标为(4,2).
点评 本题考查圆综合题、垂径定理、圆周角定理、三角形中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
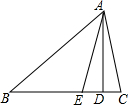 如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.
如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图所示,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是5cm.
如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
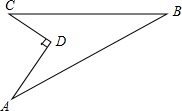 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{q}$=$\frac{p}{n}$ | B. | $\frac{p}{m}$=$\frac{n}{q}$ | C. | $\frac{q}{m}$=$\frac{n}{p}$ | D. | $\frac{m}{n}$=$\frac{p}{q}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com