
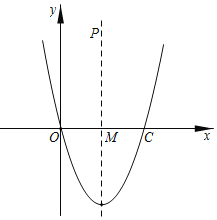
【题目】已知抛物线顶点坐标为(2,﹣4),且与x轴交于原点和点C,对称轴与x轴交点为M.
(1)求抛物线的解析式;
(2)A点在抛物线上,且A点的横坐标为﹣2,在抛物线对称轴上找一点B,使得AB与CB的差最大,求B点的坐标;
(3)P点在抛物线的对称轴上,且P点的纵坐标为8.探究:在抛物线上是否存在点Q使得O、M、P、Q四点共圆,若存在求出Q点坐标;若不存在请说明理由.
【答案】(1)抛物线的解析式为y=x2﹣4x;(2)点B(2,﹣12);(3)Q(5,5)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据顶点设出顶点坐标,再将原点的坐标代入即可得出答案;
(2)先求出A的坐标,根据三角形边的性质得出点O,A的直线与抛物线的对称轴的交点为点B,写出OA的解析式,即可得出答案;
(3)根据题意求出点P的坐标,根据四点共圆得出点Q在Rt△OMP外接圆上并设出Q的坐标,结合函数解析式以及点Q到OP的中点的距离列出方程组,解方程组,即可得出答案.
解:(1)∵抛物线顶点坐标为(2,﹣4),
∴设抛物线的解析式为y=a(x﹣2)2﹣4,
∵抛物线过原点,
∴0=a(0﹣2)2﹣4,
∴a=1,
∴抛物线的解析式为y=(x﹣2)2﹣4=x2﹣4x;
(2)由(1)知,抛物线的解析式为y=x2﹣4x,
令y=0,则x2﹣4x=0,
∴x=0或x=4,
∴C(4,0),
∵A点的横坐标为﹣2,
∴y=4﹣4×(﹣2)=12,
∴A(﹣2,12),
而抛物线的对称轴为x=2,
∴点C(4,0)关于抛物线的对称轴x=2的对称点为O(0,0),
则过点O,A的直线与抛物线的对称轴的交点为点B,理由是三角形三边关系定理之两边之差小于第三边,
∵A(﹣2,12),
∴直线OA的解析式为y=﹣6x,
当x=2时,y=﹣12,
∴点B(2,﹣12);
(3)由(2)知,抛物线的对称轴为直线x=2,
∴P(2,8),
∵抛物线的对称轴与x轴交点为M,
∴M(2,0),
∴∠OMP=90°,
∵点O、M、P、Q四点共圆,则点Q在Rt△OMP外接圆上,
∴点Q到OP的中点的距离等于半径![]() OP=
OP=![]() ,而OP的中点坐标为(1,4),
,而OP的中点坐标为(1,4),
由(1)知,抛物线的解析式为y=x2﹣4x,设Q坐标为(m,n),则m2﹣4m=n①,
∴(m﹣1)2+(n﹣4)2=17②,
∴m2﹣2m+n2﹣8n=0,
而m2﹣2m+(m2﹣4m)2﹣8(m2﹣4m)=m2﹣2m+m2(m﹣4)2﹣8m(m﹣4)
=m[m﹣2+m(m﹣4)2﹣8(m﹣4)]=m[(m﹣5)+(m﹣5)(m﹣4)2+5(m﹣4)2﹣8(m﹣5)+3﹣8]
=m{(m﹣5)+(m﹣5)(m﹣4)2+5[(m﹣5)2+2(m﹣5)+1]﹣8(m﹣5)﹣5}
=m[(m﹣5)+(m﹣5)(m﹣4)2+5(m﹣5)2+10(m﹣5)﹣8(m﹣5)]
=m(m﹣5)[1+(m﹣4)2+5(m﹣5)+2]
=m(m﹣5)(m2﹣3m﹣6)
∴m(m﹣5)(m2﹣3m﹣6)=0,
∴m=0(舍)或m=5或m2﹣3m﹣6=0,
∴m=5或m=![]() ,
,
∴Q(5,5)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
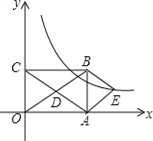
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视举办的《主持人大赛》受到广泛的关注.某中学学生会就《主持人大赛》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
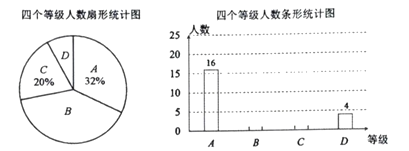
(1)本次被调查对象共有 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 .
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表),求所选取的这两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有600名学生,在体育中考前进行了一次模拟体测.从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
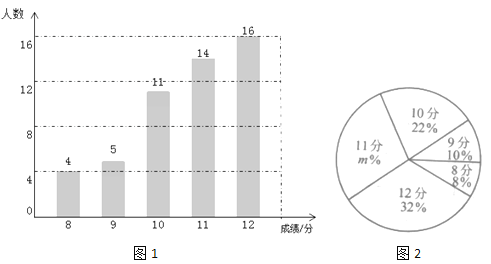
(Ⅰ)本次抽取到的学生人数为 ,图2中![]() 的值为 ;
的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
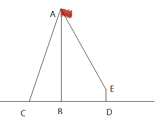
【题目】数学活动课上老师带领全班学生测量旗杆高度.如图垂直于地面的旗杆顶端A垂下一根绳子.小明同学将绳子拉直钉在地上,绳子末端恰好在点C处且测得旗杆顶端A的仰角为75°;小亮同学接着拿起绳子末端向前至D处,拉直绳子,此时测得绳子末端E距离地面1.5 m且与旗杆顶端A的仰角为60°根据两位同学的测量数据,求旗杆AB的高度.(参考数据:sin75°≈0.97,cos75°≈0.26,sin60°≈0.87,结果精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和2015年我省财政收入分别为a亿元和b亿元,则a、b之间满足的关系式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
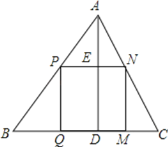
【题目】用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;乙同学说:“当正方形的一边在最短边上时,剪出的内接正方形最大”;丙同学说:“不确定,剪不出这样的正方形纸.”你认为谁说的有道理,请证明.(假设图中△ABC的三边a,b,c,且a>b>c,三边上的高分别记为ha,hb,hc)
查看答案和解析>>
科目:初中数学 来源: 题型:
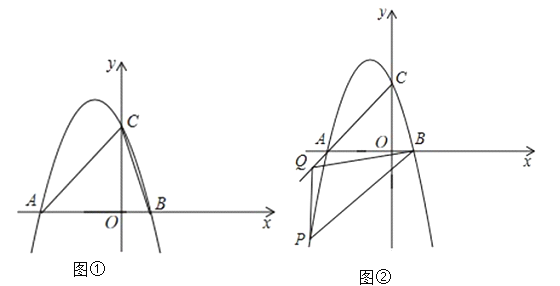
【题目】如图①,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .已知
.已知![]() 的面积是
的面积是![]() .
.
(1)求![]() 的值;
的值;
(2)在![]() 内是否存在一点
内是否存在一点![]() ,使得点
,使得点![]() 到点
到点![]() 、点
、点![]() 和点
和点![]() 的距离相等,若存在,请求出点
的距离相等,若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图②,![]() 是抛物线上一点,
是抛物线上一点,![]() 为射线
为射线![]() 上一点,且
上一点,且![]() 、
、![]() 两点均在第三象限内,
两点均在第三象限内,![]() 、
、![]() 是位于直线
是位于直线![]() 同侧的不同两点,若点
同侧的不同两点,若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com