
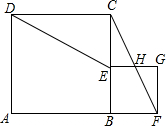
 如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.
如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.分析 (1)根据线段中点的定义可得BE=CE,再根据正方形的四条边都相等可得BC=CD,BE=BF,然后求出BF=CE,再利用“边角边”证明△BCF和△CDE全等,根据全等三角形对应边相等可得DE=CF;
(2)设CE=x,根据∠CDE的正切值表示出CD,然后求出BE,从而得到∠BCF的正切值,再根据两直线平行,内错角相等可得∠BCF=∠GFH,然后根据等角的正切值相等解答即可.
解答 (1)证明:∵E是BC的中点,
∴BE=CE,
在正方形ABCD和正方形BFGE中,BC=CD,BE=BF,
∴BF=CE,
在△BCF和△CDE中,$\left\{\begin{array}{l}{BC=CD}\\{∠CBF=∠DCE=90°}\\{BF=CE}\end{array}\right.$,
∴△BCF≌△CDE(SAS),
∴DE=CF;
(2)解:设CE=x,∵∠CDE=30°,
∴tan∠CDE=$\frac{x}{CD}$=$\frac{\sqrt{3}}{3}$,
∴CD=$\sqrt{3}$x,
∵正方形ABCD的边BC=CD,
∴BE=BC-CE=$\sqrt{3}$x-x,
∵正方形BFGE的边长BF=BE,
∴tan∠BCF=$\frac{BF}{BC}$=$\frac{\sqrt{3}x-x}{\sqrt{3}x}$=$\frac{3-\sqrt{3}}{3}$,
∵正方形BGFE对边BC∥GF,
∴∠BCF=∠GFH,
∵tan∠GFH=$\frac{HG}{GF}$,
∴$\frac{HG}{GF}$=$\frac{3-\sqrt{3}}{3}$.
点评 本题考查了正方形的性质,全等三角形的判定与性质,锐角三角函数,(1)熟练掌握三角形全等的判定方法并准确确定出全等三角形是解题的关键,(2)用CE表示出两个正方形的边长是解题的关键,也是本题的难点.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{k^2}{x}$(x<0,k是不等于0的常数)图象上一点,AO的延长线交函数y=$\frac{1}{x}$(x>0)的图象于点C.点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C′′.连结CC′,交x轴于点B,连结AB,AA′,A′C′,若△ABC的面积等于2,则四边形A A′C′C′′的面积等于( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{k^2}{x}$(x<0,k是不等于0的常数)图象上一点,AO的延长线交函数y=$\frac{1}{x}$(x>0)的图象于点C.点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C′′.连结CC′,交x轴于点B,连结AB,AA′,A′C′,若△ABC的面积等于2,则四边形A A′C′C′′的面积等于( )| A. | 7 | B. | 8 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.
如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com