
 如图,在平行四边形ABCD中,AB=5cm,BC=8cm,∠B=60°,G是CD的中点,E是边AD上的动点EG的延长线与BC的延长线交于点F,连结CE,DF.
如图,在平行四边形ABCD中,AB=5cm,BC=8cm,∠B=60°,G是CD的中点,E是边AD上的动点EG的延长线与BC的延长线交于点F,连结CE,DF.分析 (1)欲证明四边形CEDF是平行四边形,只要证明CG=GD,GF=GE或CF=ED即可.
(2)当CE⊥AD时,四边形CEDF是矩形,在RT△CED中求出ED即可解决问题.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴CF∥ED,ED,
∴∠FCG=∠EDG,
∵G是CD的中点,
∴CG=DG,
∵∠CGF=∠DGE,
∴△FCG≌△EDG,
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形.
(2)解:当CE⊥AD时,∠CED=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
在RT△CED中,∵CD=AB=5,∠DCE=∠B=60°,
∴ED=$\frac{1}{2}$CD=$\frac{5}{2}$,
∵AD=BC=8,
∴AE=AD-ED=8-$\frac{5}{2}$=5.5.
故答案为5.5.
点评 本题考查平行四边形的性质、矩形的判定和性质、直角三角形30度角性质等知识,解题的关键是熟练掌握平行四边形的判定和性质以及矩形的判定和性质,属于中考常考题型.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源:2017届重庆市九年级3月月考数学试卷(解析版) 题型:填空题
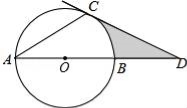
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
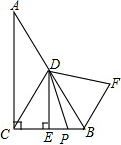 【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.
【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
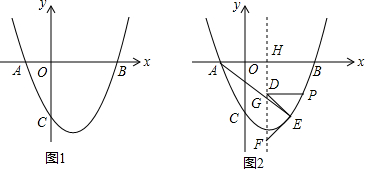 在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com