
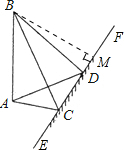
 BDE=105°,∠ADE=30°,继续往下走了5米到达C处,测得∠ACE=60°,∠BCE=120°.
BDE=105°,∠ADE=30°,继续往下走了5米到达C处,测得∠ACE=60°,∠BCE=120°.
|
| x |
| tan60° |
| x | ||
|
| x |
| 1.7 |
| x |
| tan75° |
| x |
| 3.7 |
| x |
| 1.7 |
| x |
| 3.7 |
| x |
| sin75° |
| 15.7 |
| 0.97 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
| 5 |
| 3 |
 基础上,将迎水坡面AB的坡度进行修改,修改后的迎水坡面AE的坡度i=
基础上,将迎水坡面AB的坡度进行修改,修改后的迎水坡面AE的坡度i=| 5 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 BDE=105°,∠ADE=30°,继续往下走了5米到达C处,测得∠ACE=60°,∠BCE=120°.
BDE=105°,∠ADE=30°,继续往下走了5米到达C处,测得∠ACE=60°,∠BCE=120°.查看答案和解析>>
科目:初中数学 来源:2011年湖北省黄冈市中考数学试卷(样卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com