
分析 (1)先算零指数幂,绝对值,负整数指数幂,乘方,再计算加减法即可求解;
(2)方程两边都乘以(x+3)(x-3)得到12-2(x+3)=x-3,解得x=3,然后进行检验确定分式方程的解.
解答 解:(1)(π-$\sqrt{3}$)0-|$-\frac{2}{5}$|×$(-\frac{2}{5})$-1-(-1)2007-($\frac{1}{2}$)-3
=1$-\frac{2}{5}$×(-$\frac{5}{2}$)-(-1)-8
=1+1+1-8
=-5;
(2)$\frac{12}{{x}^{2}-9}$-$\frac{2}{x-3}$=$\frac{1}{x+3}$,
去分母得:12-2(x+3)=x-3,
去括号得:12-2x-6=x-3,
移项合并得:3x=9,
解得:x=3,
经检验x=3是增根,
故原分式方程无解.
点评 本题考查了解分式方程:先去分母,把分式方程转化为整式方程,再解整式方程,然后把整式方程的解代入分式方程进行检验,最后确定分式方程的解.同时考查了实数的运算,


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
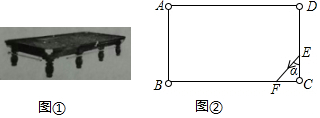
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
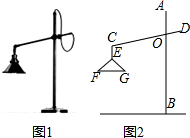 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为14cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为14cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
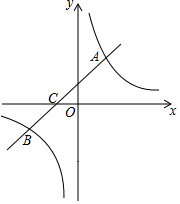 如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).
如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com