
如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的关系,并说明理由.

科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:解答题
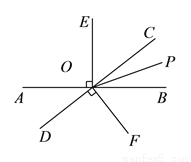
如图,直线 与
与 相交于点
相交于点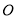 ,
, 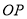 是
是 的平分线,
的平分线, 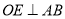 ,
,  .
.
(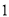 )图中除直角外,还有相等的角吗?请写出三对.
)图中除直角外,还有相等的角吗?请写出三对.
( )如果
)如果 ,求
,求 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:单选题
如图,双曲线 (k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为( )
(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:单选题
小芳在纸上画了大小不等的两个圆,并量得小圆的半径为5cm.如果大圆的半径比小圆的半径多acm,则大圆面积比小圆面积多( )
A. 25πcm2 B. πa2cm2
C. π(a+5)2cm2 D. [π(a+5)2-25π]cm2
D 【解析】根据题意可知大圆的半径是(a+5)cm,所以大圆面积比小圆面积多[π(a+5)2-25π]cm2, 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:单选题
按如图所示的运算程序,能使输出结果为3的x,y的值是( )

A. x=5,y=-2 B. x=3,y=-3
C. x=-4,y=2 D. x=-3,y=-9
D 【解析】试题分析:根据运算程序列出方程,再根据二元一次方程的解的定义对各选项分析判断利用排除法求解.故答案选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:填空题
如图①所示的∠AOB纸片,OC平分∠AOB,如图②,把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE= ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为80°,则∠AOB=____°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为80°,则∠AOB=____°.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:单选题
如图,长度为18cm的线段AB的中点为M,点C是线段MB的一个三等分点,则线段AC的长为( )

A. 3cm B. 6cm C. 9cm D. 12cm
D 【解析】∵M是线段AB的中点, ∴BM=AB. 又∵AB=18cm, ∴BM=9cm, ∵C是线段BM的三等分点, ∴BC=BM=6cm, ∴AC=AB-BC=12cm. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:填空题
关于x方程(m+1)x|m+2|+3=0是一元一次方程,那么m=______.
﹣3. 【解析】∵关于x方程(m+1)x|m+2|+3=0是一元一次方程, ∴ ,解得: . 故答案为: .查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(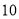 分)如图,抛物线
分)如图,抛物线 的顶点为
的顶点为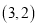 .
.
(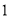 )求抛物线
)求抛物线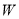 的函数表达式.
的函数表达式.
( )若抛物线形
)若抛物线形 与
与 关于
关于 轴对称,求抛物线
轴对称,求抛物线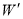 的函数表达式.
的函数表达式.
( )在(
)在( )的基础上,设
)的基础上,设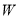 上的点
上的点 、
、 始终与
始终与 上的点
上的点 、
、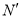 分别关于
分别关于 轴对称,是否存在点
轴对称,是否存在点 、
、 (
( 、
、 分别位于抛物线对称轴两侧,且
分别位于抛物线对称轴两侧,且 在
在 的左侧),使四边形
的左侧),使四边形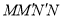 为正方形?
为正方形?
若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com