练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2013•黄石）在计数制中，通常我们使用的是“十进位制”，即“逢十进一”，而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为一天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据．已知二进位制与十进位制比较如下表：
    十进位制 0 1 2 3 4 5 6 …
    二进位制 0 1 10 11 100 101 110 …
    请将二进位制数10101010（二）写成十进位制数为
    170
    170
    ．
    分析：根据二进制的意义即可化成十进制，从而求解．
    解答：解：10101010（二）=27+25+23+2=128+32+8+2=170．
    故答案是：170．
    点评：本题考查了有理数的运算，理解二进制的意义是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

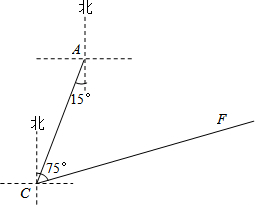    （2013•黄石）高考英语听力测试期间，需要杜绝考点周围的噪音．如图，点A是某市一高考考点，在位于A考点南偏西15°方向距离125米的C处有一消防队．在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火．已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由．（
    		3
    取1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•黄石）如图1，点C将线段AB分成两部分，如果
    AC
    AB
    =
    BC
    AC
    ，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
    S1
    S
    =
    S2
    S1
    ，那么称直线l为该图形的黄金分割线．
    （1）如图2，在△ABC中，∠A=36°，AB=AC，∠C的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
    （2）若△ABC在（1）的条件下，如图3，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
    （3）如图4，在直角梯形ABCD中，∠D=∠C=90°，对角线AC、BD交于点F，延长AB、DC交于点E，连接EF交梯形上、下底于G、H两点，请问直线GH是不是直角梯形ABCD的黄金分割线，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•黄石模拟）在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC，若三角形ABC的边长为1，AE=2，则CD的长为
    1或3
    1或3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•黄石模拟）4月20日8时2分，四川省雅安市芦山县发生了7.0级地震，当地的部分房屋严重受损，上万灾民无家可归，灾情牵动亿万中国人的心．某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地，若用大、小两种货车共20辆，恰好能一次性运完这批物资．已知这两种货车的载重量分别为16吨/辆和10吨/辆，运往甲、乙两地的运费如下表：
               车 型
    运往地    		 甲 地（元/辆） 乙 地（元/辆）
    大货车 720 800
    小货车 500 650
    （1）求这两种货车各用多少辆？
    （2）如果安排9辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为a辆，前往甲、乙两地的总运费为w元，求出w与a的函数关系式（写出自变量的取值范围）；
    （3）在（2）的条件下，若运往甲地的物资不少于132吨，请你设计出使总运费最少的货车调配方案，并求出最少总运费．

    查看答案和解析>>

    同步练习册答案