
分析 依据等式的性质由m2-6m-1=0得到2m2-6m=1+m2,$m-\frac{1}{m}=6$,故此所求代数式=1+m2+$\frac{1}{{m}^{2}}$,然后利用完全平方公式科将所求代数式变形为1$+(m-\frac{1}{m})^{2}$+2,最后代入数值进行计算即可.
解答 解:由m2-6m-1=0得;2m2-6m=1+m2,$m-\frac{1}{m}=6$,
∴2m2-6m+$\frac{1}{m^2}$=1+m2+$\frac{1}{{m}^{2}}$=1$+(m-\frac{1}{m})^{2}$+2=1+62+3=39.
故答案为:39.
点评 本题主要考查的是完全平方公式的应用、等式的性质,由m2-6m-1=0得到2m2-6m=1+m2是解题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
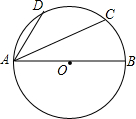 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )| A. | 20° | B. | 22° | C. | 24° | D. | 26° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| $\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$ | 理由: |
| $\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$ | |
| $\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$ | |
| … | |
| $\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 第一周 | 第二周 | 清仓 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(个) | 200 | 200+10x | 400-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
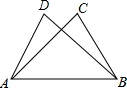 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com