
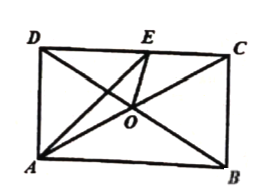
【题目】如图,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,给出以下结论:①
,给出以下结论:①![]() 为等腰直角三角形;②
为等腰直角三角形;②![]() 为等边三角形;③
为等边三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
由矩形的性质可得AO=CO=DO=BO,∠DAB=∠ABC=∠DCB=∠CDA=90°,AD∥BC,AB∥CD,由角平分线的性质和平行线的性质可判断①,由锐角三角函数可求∠ACD=30°,即可判断②,由三角形内角和定理可求∠DOE的度数,即可判断③④,由直角三角形的性质可求CE的长,即可判断⑤.
∵四边形ABCD是矩形
∴AO=CO=DO=BO,∠DAB=∠ABC=∠DCB=∠CDA=90°,AD∥BC,AB∥CD
∵AE平分∠BAD
∴∠DAE=∠EAB=45°
∵AB∥CD
∴∠DEA=∠EAB=45°
∴∠DEA=∠DAE=45°
∴AD=DE,且∠ADE=90°
∴△ADE是等腰直角三角形
故①正确
∵AD=![]() AC,∠ADC=90°
AC,∠ADC=90°
∴∠ACD=30°
∴∠OCB=60°,且OB=OC
∴△OBC是等边三角形
故②正确
∵△OBC是等边三角形
∴OB=OC=BC
∴OD=OA=AD=OC=OB
∴∠ODA=∠OAD=∠DOA=60°,∠OCD=∠ODC=30°,且OD=DE
∴∠DOE=![]() =75°
=75°
故③错误
∵∠EAC=∠OAD∠DAE=15°,∠EOC=∠DOC∠DOE=180°∠DOA75°=120°75°=45°
∴∠EOC=3∠EAC
故④正确
∵∠ACD=30°,
∴AD=![]() AC,AC=2AD
AC,AC=2AD
∴CD=![]() =
=![]() AD,且DE=DO=AD
AD,且DE=DO=AD
∴CE=![]() ADAD≠DE
ADAD≠DE
∴OE不是△ACD的中位线,
故⑤错误
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中
中![]() ,其中
,其中![]() ;
;
(1)求线段![]() 的长(用
的长(用![]() 和
和![]() 的代数式表示);
的代数式表示);
(2)如图1,若![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 到
到![]() 和BC的距离相等,
和BC的距离相等,![]() ,连接
,连接![]() ,求
,求![]() 的长;
的长;
(3)如图2,若![]() 为
为![]() 的中点,
的中点,![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() 和
和![]() ,求EF的值;
,求EF的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB= ![]() .
.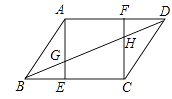
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .A课程成绩的频数分布直方图如下(数据分成6组:
.A课程成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
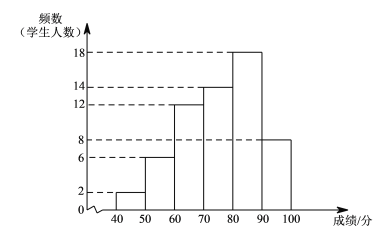
![]() .A课程成绩在
.A课程成绩在![]() 这一组是:
这一组是:
70 71 71 71 76 76 77 78 ![]()
![]() 79 79 79
79 79 79 ![]()
![]() .A,B两门课程成绩的平均数、中位数、众数如下:
.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过![]() 分的人数.
分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比思想就是根据已经学习过的知识,类比探究新知识的思想方法.我们在探究矩形、菱形、正方形等问题中的数量关系时,经常用到类比思想.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() 连接
连接![]() .
.
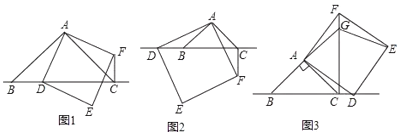
(1)(观察猜想)如图①,当点![]() 在线段
在线段![]() 上时;
上时;
①![]() 与
与![]() 的位置关系为: ;
的位置关系为: ;
②![]() 之间的数量关系为: ;(将结论直接写在横线上)
之间的数量关系为: ;(将结论直接写在横线上)
(2)(数学思考)如图②,当点![]() 在线段
在线段![]() 的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)(拓展延伸)如图③,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() 请直接写出
请直接写出![]() 的长.(提示: .过
的长.(提示: .过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() 于
于![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2 ![]() =(1+
=(1+ ![]() )2 , 我们来进行以下的探索:
)2 , 我们来进行以下的探索:
设a+b ![]() =(m+n
=(m+n ![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b ![]() =m2+2n2+2mn
=m2+2n2+2mn ![]() ,∴a=m+2n2 , b=2mn
,∴a=m+2n2 , b=2mn
, 这样就得出了把类似a+b ![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b ![]() =(m﹣n
=(m﹣n ![]() )2 , 用含m,n的式子分别表示a,b,得a= , b=;
)2 , 用含m,n的式子分别表示a,b,得a= , b=;
(2)利用上述方法,找一组正整数a,b,m,n填空:﹣ ![]() =(﹣
=(﹣ ![]() )2
)2
(3)a﹣4 ![]() =(m﹣n
=(m﹣n ![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、AD是⊙O的弦,点C是DO的延长线与弦AB的交点,∠ABO=30°,OB=2.
(1)求弦AB的长;
(2)若∠D=20°,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.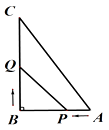
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com