
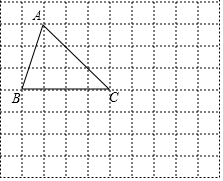
 如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.(注:顶点在网格线交点处的三角形叫做格点三角形)
如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.(注:顶点在网格线交点处的三角形叫做格点三角形)分析 (1)利用面积法计算AC边上的高;
(2)取BC的中点E,过E作DE∥AB交AC于F,则△DEC满足条件;或延长BC到E′使CE′=$\frac{1}{2}$BC,作E′D′∥AB交AC的延长线于D′,则△D′E′C满足条件.
解答 解:(1)设AC边上的高为h,
则$\frac{1}{2}$AC•h=$\frac{1}{2}$BC•3,
所以h=$\frac{3×4}{3\sqrt{2}}$=2$\sqrt{2}$,
故答案为2$\sqrt{2}$;
(2)如图,△DEC和△D′E′C为所作.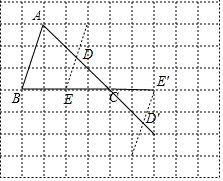
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
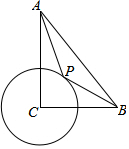 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2$\sqrt{17}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com