
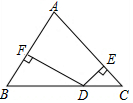
 如图,在△ABC中,∠B=63°,∠C=45°,DE⊥AC于E,DF⊥AB于F,那么∠EDF=108°.
如图,在△ABC中,∠B=63°,∠C=45°,DE⊥AC于E,DF⊥AB于F,那么∠EDF=108°. 科目:初中数学 来源: 题型:选择题
| A. | y=(x-3)2 | B. | y=x2+3 | C. | y=(x+3)2 | D. | y=x2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 地名 | 时间 |
| 王家庄 | 9:00 |
| 青山 | 12:00 |
| 秀水 | 14:00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{8}$=2$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
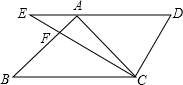 将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com