
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1 , B1 , C1 , 使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 , 记其面积为S1;第二次操作,分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使得A2B1=2A1B1 , B2C1=2B1C1 , C2A1=2C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , 记其面积为S2 , 则S2=。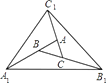
科目:初中数学 来源: 题型:
【题目】2013年3月28是第18个全国中小学生安全教育日.某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”.请回答:

(1)参加全校安全知识测试的学生有 名;
(2)中位数落在 分数段内;
(3)若用各分数段的中间值(如5.5~10.5的中间值为8)来代替本段均分,请你估算本次测试成绩全校平均分约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC , BD平分∠ABC . 过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E , BC交DE于点F , 连接CE . 求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com