
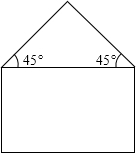
 用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积. | 2 |
20-(4+2
| ||
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| b |
| 2a |
| 10 | ||
3+2
|
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源:2011-2012学年苏州市区九年级上学期期末考试数学卷 题型:填空题
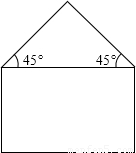
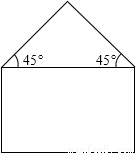
(本题满分6分)用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(18):2.6 何时获得最大利润(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com