
 与抛物线
与抛物线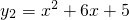 关于y轴对称,并与y轴交于点M,与x轴交于A、B两点.
关于y轴对称,并与y轴交于点M,与x轴交于A、B两点.
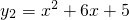 来说,令x=0,则y=5,
来说,令x=0,则y=5,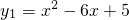 .…
.… ,
, CB•OM=
CB•OM= ×2×5=5,
×2×5=5, ,
, ×5
×5 -CH=5,
-CH=5,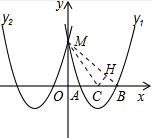
 ,
,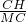 =
=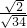 =
=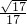 .
. ,0).
,0). ,5),P5(-
,5),P5(- ,5),P6(
,5),P6( ,-5).
,-5). ,5),P5(-
,5),P5(- ,5),P6(
,5),P6( ,-5).
,-5).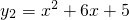 ,令x=0,可得y=5,从而可得出点M的坐标,令y=0,可求出x1=-1,x2=-5,从而得出抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),结合轴对称的知识,可设y1=a(x-1)(x-5),将点M(0,5)代入,即可得出解析式;
,令x=0,可得y=5,从而可得出点M的坐标,令y=0,可求出x1=-1,x2=-5,从而得出抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),结合轴对称的知识,可设y1=a(x-1)(x-5),将点M(0,5)代入,即可得出解析式;

科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 米,旗杆AB高为3米,C点的垂
米,旗杆AB高为3米,C点的垂 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:河南省期中题 题型:解答题
 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知m、n是方程![]() 的两个实数根,且m<n,抛物线
的两个实数根,且m<n,抛物线![]() 的图像经过点A(m,0)、B(0,n).
的图像经过点A(m,0)、B(0,n).
 (1)求这个抛物线的解析式;
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的
顶点为D,试求出点C、D的坐标和△BCD的面积;
(注:抛物线![]() 的顶点坐标为
的顶点坐标为
![]()
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛
物线交于H点,若直线BC把△PCH分成面积之比
为2:3的两部分,请求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:解答题
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com