
分析 (1)根据a=1可判断抛物线的开口方向,然后利用配方法可求得抛物线的对称轴和顶点坐标;
(2)根据抛物线的顶点坐标和抛物线开口方向即可判断;
(3)根据根与系数的关系、完全平方公式求得|x1=x2|=2$\sqrt{3}$,然后利用三角形的面积公式可求得△ABD的面积=3$\sqrt{3}$.
解答 解:(1)∵a=1,
∴抛物线的开口向下.
y=x2-6mx+9m2-3=(x-3m)2-3,
∴抛物线的对称轴为x=3m,顶点坐标为(3m,-3).
(2)∵抛物线顶点坐标为(3m,-3),
∴顶点在x轴下方.
又∵抛物线开口向上,
∴不论m为何值,该抛物线与x轴有两个不同的交点.
(3)由根与系数的关系可知:x1+x2=6m,x1x2=9m2-3.
∴AB=|x1=x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(6m)^{2}-4(9{m}^{2}-3)}$=$\sqrt{12}$=2$\sqrt{3}$.
∴△ABD的面积=$\frac{1}{2}×AB×|-3|$=$\frac{1}{2}×2\sqrt{3}×3$=3$\sqrt{3}$.
∴不论m为何值,△ABD的面积为定值.
点评 本题主要考查的是抛物线与x轴的交点问题,掌握二次函数与一元二次方程的关系是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
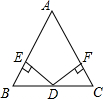 如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
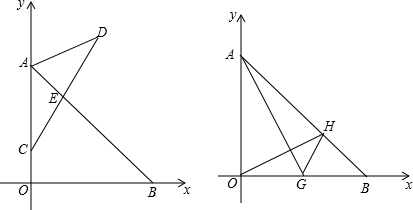
 如图,点O为平面直角坐标系的原点,在?ABCD中,A(0,4),B(2,0),C(4,0),过A作直线AE交x轴FE点,tan∠AEO=$\frac{4}{3}$
如图,点O为平面直角坐标系的原点,在?ABCD中,A(0,4),B(2,0),C(4,0),过A作直线AE交x轴FE点,tan∠AEO=$\frac{4}{3}$ 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
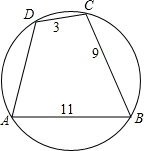 已知圆内接四边形ABCD中,AB=11,BC=9,CD=3,如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$,则AD=7.
已知圆内接四边形ABCD中,AB=11,BC=9,CD=3,如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$,则AD=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com