
如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为 .

科目:初中数学 来源: 题型:
某市按以下规定收取每月的水费:用水量不超过6吨,按每吨1.2元收费;如果超过6吨,未超过部分仍按每吨1.2元收取,而超过部分则按每吨2元收费.如果某用户5月份水费平均为每吨1.4元,那么该用户5月份实际用水 吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知正方形的边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是( )

A. 0.1 B.0.2 C.0.3 D. 0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )

A. 2﹣ B.
B. C.
C.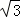 ﹣1 D. 1
﹣1 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
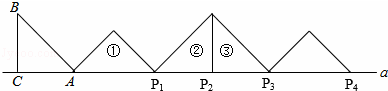
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=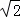 ;将位置①的三角形绕点P1
;将位置①的三角形绕点P1 顺时针旋转到位置②,可得到点P2,此时AP2=1+
顺时针旋转到位置②,可得到点P2,此时AP2=1+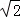 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+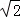 ;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .
;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)证明:△ABE≌△C1BF;
(2)证明:EA1=FC;
(3)试判断四边形ABC1D的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com