
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćPµÄ×ų±źĪŖ£Ø ![]() £©£¬µćQµÄ×ų±źĪŖ
£©£¬µćQµÄ×ų±źĪŖ ![]() £¬ĒŅ
£¬ĒŅ ![]() £¬
£¬ ![]() £¬ČōP£¬QĪŖijøö¾ŲŠĪµÄĮ½øö¶„µć£¬ĒŅøĆ¾ŲŠĪµÄŅ»×é¶Ō±ßÓėijĢõ×ų±źÖįĘ½ŠŠ£¬Ōņ³ĘøĆ¾ŲŠĪĪŖµćP£¬QµÄ”°Ļą¹Ų¾ŲŠĪ”±£¬Ķ¼2¼°Ķ¼3ÖŠµćAµÄ×ų±źĪŖ£Ø4,3£©.
£¬ČōP£¬QĪŖijøö¾ŲŠĪµÄĮ½øö¶„µć£¬ĒŅøĆ¾ŲŠĪµÄŅ»×é¶Ō±ßÓėijĢõ×ų±źÖįĘ½ŠŠ£¬Ōņ³ĘøĆ¾ŲŠĪĪŖµćP£¬QµÄ”°Ļą¹Ų¾ŲŠĪ”±£¬Ķ¼2¼°Ķ¼3ÖŠµćAµÄ×ų±źĪŖ£Ø4,3£©.
£Ø1£©ČōµćBµÄ×ų±źĪŖ£Ø-2,0£©£¬ŌņµćA£¬BµÄ”°Ļą¹Ų¾ŲŠĪ”±µÄĆ껿ĪŖ£»
£Ø2£©µćCŌŚyÖįÉĻ£¬ČōµćA£¬CµÄ”°Ļą¹Ų¾ŲŠĪ”±µÄĆ껿ĪŖ8£¬ĒóÖ±ĻßACµÄ½āĪöŹ½£»
£Ø3£©ČēĶ¼3£¬Ö±Ļß ![]() ÓėxÖį½»ÓŚµćM£¬ÓėyÖį½»ÓŚµćN£¬ŌŚÖ±ĻßMNÉĻŹĒ·ń“ęŌŚµćD£¬Ź¹µćA£¬DµÄ”°Ļą¹Ų¾ŲŠĪ”±ĪŖÕż·½ŠĪ£¬Čē¹ū“ęŌŚ£¬ĒėĒó³öµćDµÄ×ų±ź£¬Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
ÓėxÖį½»ÓŚµćM£¬ÓėyÖį½»ÓŚµćN£¬ŌŚÖ±ĻßMNÉĻŹĒ·ń“ęŌŚµćD£¬Ź¹µćA£¬DµÄ”°Ļą¹Ų¾ŲŠĪ”±ĪŖÕż·½ŠĪ£¬Čē¹ū“ęŌŚ£¬ĒėĒó³öµćDµÄ×ų±ź£¬Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
”¾“š°ø”æ
£Ø1£©18
£Ø2£©
½ā£ŗÓÉ”°Ļą¹Ų¾ŲŠĪ”±µÄ¶ØŅ壬µćCÓėµćAŌŚ¾ŲŠĪÖŠŹĒĻą¶ŌµÄ£¬
”ßµćCŌŚyÖįÉĻ£¬æÉÉčC£Ø0£¬a£©£¬
”ą|a-3|”Į4=8£¬½āµĆa=1»ņ5£¬
ŌņC£Ø0,1£©»ņ£Ø0,5£©£¬
µ±C£Ø0,1£©Ź±£¬Ö±ĻßACµÄ½āĪöŹ½y= ![]() x+1£»
x+1£»
µ±C£Ø0,5£©Ź±£¬Ö±ĻßACµÄ½āĪöŹ½y= ![]() x+5.
x+5.
£Ø3£©
½ā£ŗ“ęŌŚ.æÉÉčD£Øx, ![]() £©,
£©,
µ±A£¬DµÄĻą¹Ų¾ŲŠĪĪŖÕż·½ŠĪŹ±£¬
Ōņ|x-4|=| ![]() -3|£¬
-3|£¬
Ōņx-4= ![]() -3£¬»ņx-4=
-3£¬»ņx-4= ![]()
½āµĆx=2»ņx=10.
ŌņD£Ø2,1£©»ņ£Ø10,3£©.
”¾½āĪö”æ½ā£ŗ£Ø1£©ČēĶ¼£¬¾ŲŠĪACBDĪŖA£¬BµÄ”°Ļą¹Ų¾ŲŠĪ”±£¬
ĖüµÄĆ껿ĪŖ£Ø4+2£©”Į3=18.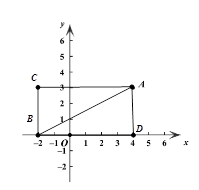



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉäĻßOAŗĶÉäĻßOBŹĒŅ»øö½ĒµÄĮ½±ß£¬Õāøö½ĒæɼĒĪŖ£Ø £©£®
A.”ĻAOB
B.”ĻBAO
C.”ĻOBA
D.”ĻOAB
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĢ½¾æ¹éÄÉĢā£ŗ
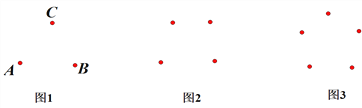
(1)ŹŌŃé·ÖĪö£ŗ
ČēĶ¼1£¬¾¹żAµćÓėB”¢CĮ½µć·Ö±š×÷Ö±Ļߣ¬æÉŅŌ×÷____________Ģõ£»Ķ¬Ńł£¬¾¹żBµćÓėA”¢CĮ½µć·Ö±š×÷Ö±Ļߣ¬æÉŅŌ×÷______________Ģõ£»¾¹żCµćÓėA”¢BĮ½µć·Ö±š×÷Ö±Ļߣ¬æÉŅŌ×÷___________Ģõ.
ĶعżŅŌÉĻ·ÖĪöŗĶ×ܽį£¬Ķ¼1¹²ÓŠ___________ĢõÖ±Ļß.
£Ø2£©ĶŲÕ¹ŃÓÉģ£ŗ
ŌĖÓĆ£Ø1£©µÄ·ÖĪö·½·Ø£¬æÉµĆ£ŗ
Ķ¼2¹²ÓŠ_____________ĢõÖ±Ļߣ»
Ķ¼3¹²ÓŠ_____________ĢõÖ±Ļߣ»
(3)Ģ½Ė÷¹éÄÉ£ŗ
Čē¹ūĘ½ĆęÉĻÓŠn(n”Ż3)øöµć£¬ĒŅĆæ3øöµć¾ł²»ŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬¾¹żĘäÖŠĮ½µć¹²ÓŠ________ĢõÖ±Ļߣ®(ÓĆŗ¬nµÄŹ½×Ó±ķŹ¾)
(4)½ā¾öĪŹĢā£ŗ
ÖŠÖ°Ąŗ£ØCBA£©2017”Ŗ”Ŗ2018Čü¼¾×÷³öÖŲ“óøÄøļ£¬±ČČü¶ÓĪ鏿Ą©³äĪŖ20Ö§£¬½ŲÖ¹2017Äź12ŌĀ21ČÕČü³Ģ¹ż°ė£¬¼“ĆæĮ½¶ÓÖ®¼ä¶¼ČüĮĖŅ»³”£¬ĒėÄć°ļÖś¼ĘĖćŅ»ĻĀŅ»¹²½ųŠŠĮĖ¶ąÉŁ³”±ČČü£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠø÷Ź½ÖŠÕżČ·µÄŹĒ£Ø £©
A. 22=(-2)2B. 33=(-3)3C. -22=|-22 |D. -33=|33 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,ŅŃÖŖÅ×ĪļĻßy=©x2+2x¾¹żŌµćO,ĒŅÓėÖ±Ļßy=x©2½»ÓŚB£¬CĮ½µć£®
£Ø1£©ĒóÅ×ĪļĻߵĶ„µćAµÄ×ų±ź¼°µćB,CµÄ×ų±ź£»
£Ø2£©ĒóÖ¤£ŗ”ĻABC=90”ć£»
£Ø3£©ŌŚÖ±ĻßBCÉĻ·½µÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP,Ź¹”÷PBCµÄĆ껿×ī“ó£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø4£©ČōµćNĪŖxÖįÉĻµÄŅ»øö¶Æµć£¬¹żµćN×÷MN”ĶxÖįÓėÅ×ĪļĻß½»ÓŚµćM£¬ŌņŹĒ·ń“ęŌŚŅŌO£¬M£¬NĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öµćNµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬PAĪŖ”ŃOµÄĒŠĻߣ¬AĪŖĒŠµć.¹żA×÷OPµÄ“¹ĻßAB£¬“¹×ćĪŖµćC£¬½»”ŃOÓŚµćB.ŃÓ³¤BOÓė”ŃO½»ÓŚµćD£¬ÓėPAµÄŃÓ³¤Ļß½»ÓŚµćE.
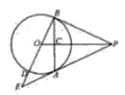
£Ø1£©ĒóÖ¤£ŗPBĪŖ”ŃOµÄĒŠĻߣ»£Ø2£©Čōtan”ĻABE=![]() £¬ĒósinEµÄÖµ.
£¬ĒósinEµÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖ±Ļßa”¢b”¢cÖŠ£¬a”Īb, b”Īc£¬ŌņÖ±ĻßaÓėÖ±ĻßcµÄ¹ŲĻµŹĒ£Ø £©
A. Ļą½»B. Ę½ŠŠC. “¹Ö±D. ²»Č·¶Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōŅ»øö¶ą±ßŠĪµÄÄŚ½ĒŗĶŠ”ÓŚĖüµÄĶā½ĒŗĶ£¬ŌņÕāøö¶ą±ßŠĪµÄ±ßŹżŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÄŚ½ÓÓŚ”ŃO£¬”ĻAµÄ¶ČŹżĪŖ60”ć£¬”ĻABC”¢”ĻACBµÄ½ĒĘ½·ÖĻß·Ö±š½»ÓŚAC”¢ABÓŚµćD”¢E£¬CE”¢BDĻą½»ÓŚµćF.ŅŌĻĀĖÄøö½įĀŪ£ŗ¢Ł![]() £»¢Ś
£»¢Ś![]() £»¢Ū
£»¢Ū![]() £»¢Ü
£»¢Ü![]() .ĘäÖŠ½įĀŪŅ»¶ØÕżČ·µÄŠņŗÅŹżŹĒ( )
.ĘäÖŠ½įĀŪŅ»¶ØÕżČ·µÄŠņŗÅŹżŹĒ( )

A. ¢Ł¢Ś B. ¢Ł¢Ū C. ¢Ū¢Ü D ¢Ś¢Ü
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com