练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    圆心角是120°的扇形的弧长为1，求内切于这个扇形的圆的周长．

     

    答案：
    解析：

    		设⊙O1与OA、OB、分别相切于C、D、E，连结O1C，则O1C⊥OA，连结OO1并延长，则必过点E．

    ∴　∠COO1=∠AOB=60°．

    设扇形的半径为R，⊙O1半径为r，

    ∵　l=且l=1，∴　R=．在Rt△COO1中，O1C=OO1 sin60°，即

    r=(R-r)×．

    解得r=(2-3)R，∴　r=(2-3)×=．∴　⊙O1的周长为2pr=2p．

    =6-9．

     


    提示：

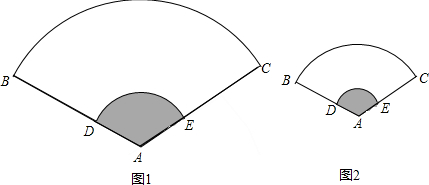
    		如图，欲求⊙O1的周长，需求⊙O1的半径，而⊙O1内切于扇形OAB，且∠AOB=120°，因此⊙O1的半径与扇形的半径有一定的关系，因为的长为1，所以利用弧长公式可求出扇形的半径．故⊙O1的半径也可求．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某校研究性学习小组在研究相似图形时，发现相似三角形的定义、判定及其性质，可以拓展到扇形的相似中去．例如，可以定义：“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”；相似扇形有性质：弧长比等于半径比、面积比等于半径比的平方…．请你协助他们探索这个问题．
    （1）写出判定扇形相似的一种方法：若
     
    ，则两个扇形相似；
    （2）有两个圆心角相等的扇形，其中一个半径为a、弧长为m，另一个半径为2a，则它的弧长为
     
    ；
    （3）如图1是一完全打开的纸扇，外侧两竹条AB和AC的夹角为120°，AB为30cm，现要做一个和它形状相同、面积是它一半的纸扇（如图2），求新做纸扇（扇形）的圆心精英家教网角和半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

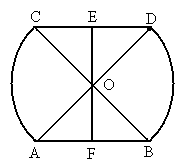
    某花园要安装一个如图所示样式的两扇门．和是以O为圆心、以AB长为半径的两条等弧，所对的圆心角为120°，AB的长是2m．AD，BC，EF相交于点O，且EF⊥CD于点E，EF⊥AB于点F．求这两扇门的面积．(结果保留两位小数)

    查看答案和解析>>

    科目：初中数学 来源：第24章《圆（下）》中考题集（53）：24.4 圆的有关计算（解析版） 题型：解答题

    某校研究性学习小组在研究相似图形时，发现相似三角形的定义、判定及其性质，可以拓展到扇形的相似中去．例如，可以定义：“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”；相似扇形有性质：弧长比等于半径比、面积比等于半径比的平方…．请你协助他们探索这个问题．
    （1）写出判定扇形相似的一种方法：若______，则两个扇形相似；
    （2）有两个圆心角相等的扇形，其中一个半径为a、弧长为m，另一个半径为2a，则它的弧长为______；
    （3）如图1是一完全打开的纸扇，外侧两竹条AB和AC的夹角为120°，AB为30cm，现要做一个和它形状相同、面积是它一半的纸扇（如图2），求新做纸扇（扇形）的圆心角和半径．

    查看答案和解析>>

    科目：初中数学 来源：第3章《圆》常考题集（35）：3.4 弧长和扇形的面积，圆锥的侧面展开图（解析版） 题型：解答题

    某校研究性学习小组在研究相似图形时，发现相似三角形的定义、判定及其性质，可以拓展到扇形的相似中去．例如，可以定义：“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”；相似扇形有性质：弧长比等于半径比、面积比等于半径比的平方…．请你协助他们探索这个问题．
    （1）写出判定扇形相似的一种方法：若______，则两个扇形相似；
    （2）有两个圆心角相等的扇形，其中一个半径为a、弧长为m，另一个半径为2a，则它的弧长为______；
    （3）如图1是一完全打开的纸扇，外侧两竹条AB和AC的夹角为120°，AB为30cm，现要做一个和它形状相同、面积是它一半的纸扇（如图2），求新做纸扇（扇形）的圆心角和半径．

    查看答案和解析>>

    科目：初中数学 来源：第3章《圆》中考题集（80）：3.4 弧长和扇形的面积，圆锥的侧面展开图（解析版） 题型：解答题

    某校研究性学习小组在研究相似图形时，发现相似三角形的定义、判定及其性质，可以拓展到扇形的相似中去．例如，可以定义：“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”；相似扇形有性质：弧长比等于半径比、面积比等于半径比的平方…．请你协助他们探索这个问题．
    （1）写出判定扇形相似的一种方法：若______，则两个扇形相似；
    （2）有两个圆心角相等的扇形，其中一个半径为a、弧长为m，另一个半径为2a，则它的弧长为______；
    （3）如图1是一完全打开的纸扇，外侧两竹条AB和AC的夹角为120°，AB为30cm，现要做一个和它形状相同、面积是它一半的纸扇（如图2），求新做纸扇（扇形）的圆心角和半径．

    查看答案和解析>>

    同步练习册答案