
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
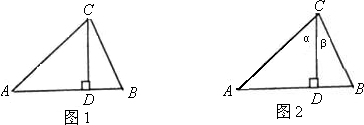
| CD |
| AC |
| 1 |
| 2 |
| CD |
| BC |
| CD |
| AC |
| CD |
| AC |
| CD |
| BC |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 4 |


科目:初中数学 来源: 题型:
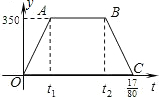 沪杭高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C(
沪杭高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C(| 17 |
| 80 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.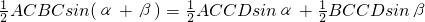 ,即
,即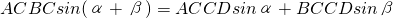 ②.
②.
查看答案和解析>>
科目:初中数学 来源:2008-2009学年山东省潍坊市高密初中学段九年级(上)期末数学试卷(解析版) 题型:解答题
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理. ,即
,即 ②.
②.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com