练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）

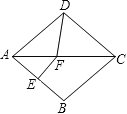
    A.50°B.60°C.70°D.80°

    【答案】B

    【解析】

    如图，连接BF，

    在菱形ABCD中，∵∠BAD=80°，

    ∴∠BAC=∠BAD=×80°=40°，∠BCF=∠DCF，BC=CD，

    ∠ABC=180°﹣∠BAD=180°﹣80°=100°．

    ∵EF是线段AB的垂直平分线，∴AF=BF，∠ABF=∠BAC=40°．

    ∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°．

    ∵在△BCF和△DCF中，BC=CD，∠BCF=∠DCF，CF=CF，∴△BCF≌△DCF（SAS）．

    ∴∠CDF=∠CBF=60°．故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将三角形ABC向左平移至点B与原点重合，得三角形A′OC′．

    （1）直接写出三角形ABC的三个顶点的坐标A　　，B　　，C　　；

    （2）画出三角形A′OC′；

    （3）求三角形ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＋∠2﹦180°,∠3﹦∠B，则DE∥BC，下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容．

    证明：

    ∵∠1＋∠2﹦180（已知），

    ∠1﹦∠4 （_________________），

    ∴∠2﹢_____﹦180°.

    ∴EH∥AB（___________________________________）．

    ∴∠B﹦∠EHC（________________________________）．

    ∵∠3﹦∠B（已知）

    ∴ ∠3﹦∠EHC（____________________）．

    ∴ DE∥BC（__________________________________）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是“过圆外一点作圆的切线”的尺规作图过程.

    请回答以下问题：

    （1）连接OA，OB，可证∠OAP =∠OBP = 90°，理由是______________________；

    （2）直线PA，PB是⊙O的切线，依据是__________________________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现代语言表述为：如图，AB为⊙O的直径，弦CD⊥AB于点E，AE = 1寸，CD = 10寸，求直径AB的长．请你解答这个问题.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为A（0，a），B（b，a），且a，b满足（a﹣3）2+|b﹣6|＝0，现同时将点A，B分别向下平移3个单位，再向左平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．

    （1）求点C，D的坐标及四边形ABDC的面积S四边形ABCD；

    （2）在y轴上是否存在一点M，连接MC，MD，使S△MCD＝S四边形ABCD？若存在这样一点，求出点M的坐标，若不存在，试说明理由；

    （3）点P是直线BD上的一个动点，连接PA，PO，当点P在BD上移动时（不与B，D重合），直接写出∠BAP，∠DOP，∠APO之间满足的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等边三角形ABC中，BC=6cm，射线AG//BC，点E从点A出发，沿射线AG以1cm/s的速度运动，同时点F从点B出发，沿射线BC以2cm/s的速度运动，设运动时间为t，当t为( )s时，以A，F，C，E为顶点的四边形是平行四边形？（ ）

    A.2B.3C.6D.2或6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

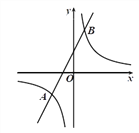
    【题目】如图，在平面直角坐标系中，一次函数与反比例函数交于点， ．

    （1）分别求出反比例函数和一次函数的表达式；

    （2）根据函数图象，直接写出不等式的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

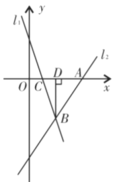
    【题目】综合与探究： 如图，直线的表达式为，与轴交于点，直线交轴于点，，与交于点，过点作轴于点，．

    （1）求点的坐标；

    （2）求直线的表达式；

    （3）求的值；

    （4）在轴上是否存在点，使得？若存在，请直接写出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案