
����Ŀ�����꼶�߰ࡰ��ѧ��ȤС�顱�Ժ����ĶԳƱ任����̽����������̽���������ù��̣��벹��������
��1���������֣���������y=|x|��ͼ��ʱ�������˷ֶκ����İ취���ú���ת��Ϊy= ![]() ��������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ��
��������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ��
��2�����̽��
������y=|x��1|��ͼ����ת��Ϊ�ֶκ��� �� Ȼ��ֱ��������κ�����ͼ������С꿣���������ƽ���ϵ���Գ�֪ʶ���Ѻ���y=x��1��x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y=|x��1|��ͼ����ͼ��ʾ��
��3����չ���
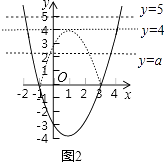
��ͼ2��ͼ�Ǻ���y=x2��2x��3��ͼ������ԭ����ϵ������y=|x2��2x��3|��ͼ��
��4��ʵ������
�ٺ��� ![]() ��ͼ����x���������㣬��Ӧ����|x2��2x��3|=0����ʵ����
��ͼ����x���������㣬��Ӧ����|x2��2x��3|=0����ʵ����
�ں��� ![]() ��ͼ����ֱ��y=5�������㣬��Ӧ����|x2��2x��3|=5����ʵ����
��ͼ����ֱ��y=5�������㣬��Ӧ����|x2��2x��3|=5����ʵ����
�ۺ��� ![]() ��ͼ����ֱ��y=4�������㣬��Ӧ����
��ͼ����ֱ��y=4�������㣬��Ӧ���� ![]() ����ʵ����
����ʵ����
�ܹ���x�ķ��� ![]() ��4��ʵ��ʱ��a��ȡֵ��Χ�� ��
��4��ʵ��ʱ��a��ȡֵ��Χ�� ��
���𰸡�
��1��
�⣺��ͼ1��
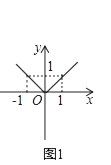
��2��![]()
��3��
�⣺�Ѻ���y=x2��2x��3��ͼ����x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y=|x2��2x��3|��ͼ����ͼ2��
��4��2��2��2��2��3��3��0��a��4
���������⣺��2.�����̽��
������y=|x��1|��ͼ����ת��Ϊ�ֶκ���y= ![]() ����4��ʵ�����âٺ���y=|x2��2x��3|��ͼ����x���� 2�����㣬��Ӧ����|x2��2x��3|=0��2��ʵ�����ں���y=|x2��2x��3|��ͼ����ֱ��y=5�� 2�����㣬��Ӧ����|x2��2x��3|=5��2��ʵ�����ۺ���y=|x2��2x��3|��ͼ����ֱ��y=4��3�����㣬��Ӧ����|x2��2x��3|=4��3��ʵ�����ܹ���x�ķ���|x2��2x��3|=a��4��ʵ��ʱ��a��ȡֵ��Χ�� 0��a��4��
����4��ʵ�����âٺ���y=|x2��2x��3|��ͼ����x���� 2�����㣬��Ӧ����|x2��2x��3|=0��2��ʵ�����ں���y=|x2��2x��3|��ͼ����ֱ��y=5�� 2�����㣬��Ӧ����|x2��2x��3|=5��2��ʵ�����ۺ���y=|x2��2x��3|��ͼ����ֱ��y=4��3�����㣬��Ӧ����|x2��2x��3|=4��3��ʵ�����ܹ���x�ķ���|x2��2x��3|=a��4��ʵ��ʱ��a��ȡֵ��Χ�� 0��a��4��
�ʴ�Ϊy= ![]() ��2��2��2��2��3��3��0��a��4��
��2��2��2��2��3��3��0��a��4��
��1��������㷨��y=|x|��ͼ��2�����ݾ���ֵ�����壬���÷������۵�˼��д���ֶκ�������3���루2��������ͼ��ķ���һ�����Ѻ���y=x2��2x��3��ͼ����x�����沿�֣���x����з��ۿɵõ�����y=|x2��2x��3|��ͼ��4�����û�����ͼ��ͨ��ȷ��y=|x2��2x��3|��ͼ����ֱ��y=a�Ľ������������⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ʦ���Լ��ν̵�55����������һ�������ײ��ԣ����涨�����ɼ�Ϊ16��ϸ��±��������ȡ��10��������A��B������Եijɼ���ϸ���IJ�ֵ���Ⱥϸ���������Ϊ�����ٵ�����Ϊ������
A �� | -1.5 | +1.5 | -1 | -2 | -2 |
B�� | +1 | +3 | -3 | +2 | -3 |
��1����������55�������кϸ��������Լ�Ƕ��٣�
��2��ͨ����صļ��㣬˵���ĸ���ijɼ��ȽϾ��ȣ�
��3�����پٳ���������˵��A��ɼ�����B��ɼ������ҳ�һ��������˵��B�����A�顣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1���ڡ�ABC�У���ACB��2��B����C��90�㣬ADΪ��BAC��ƽ���߽�BC��D����֤��AB��AC��CD������ʾ����AB�Ͻ�ȡAE��AC������DE��



��2����ͼ2������C��90��ʱ�������������䣬�߶�AB��AC��CD����������������ϵ��ֱ��д�����������Ҫ֤����
��3����ͼ3������ACB��90�㣬��ACB��2��B ��ADΪ��ABC����ǡ�CAF��ƽ���ߣ���BC���ӳ����ڵ�D�����߶� AB��AC��CD����������������ϵ��д����IJ��룬������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��֯����ְ������ǰ��ij���������ιۣ��μ���Ա��70�ˣ����ξ���涨������Ʊÿ��60Ԫ�����Żݣ�����ɽ��������������㰲�ŵĹ۹�������۹��С�ͳ������ͳ����࣬�ֱ�ɹ�4����11���˿ͳ�������С�ͳ�ÿ���շ�60Ԫ�����ͳ�ÿ���շ�10Ԫ����70����������ÿ�����Ҳι��������ܷ��ò�����5000Ԫ���ʾ��㰲�ŵ�С�ͳ������ͳ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���̶Ӵ�A��������ر�ƫ��67��������һ����·AD����BD·�γ������������ı䷽����B���ر�ƫ��23���ķ��������BC�Σ�����C���ָı䷽��C�������CE�Σ���ʹ����·��CE��AB����ECBӦΪ���ٶȣ���˵�����ɣ���ʱCE��BC��������λ�ù�ϵ��
������С�ղ������Ľ�����������������
�⣺����֪�������� ��
�á�1=��A=67��
���ԣ���CBD=23��+67��=�� ���㣻
������ ��
����ECB+��CBD=�� ����ʱ���ɵ�CE��AB��
���ԡ�ECB=�� ��
��ʱCE��BC��λ�ù�ϵΪ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���ͼ��ʾ��ͼ�Σ��ش��������⣺
(1) ͼ�еĵ㱻�߶θ����ֳ��IJ㣬��һ����1���㣬�ڶ�����3���㣬��������5���㣬���IJ���___________���㣻
(2) ���Ҫ���������ȥ����ô�������________�㣬 ��10����_________�㣻
(3) ijһ������77���㣬���֪�����ǵ�_________�㣻
(4) ��һ����ڶ���ĺ���__________��ǰ����ĺ���_________��ǰ�IJ��Ϊ____________��
����û�з���ʲô����?
��������Ʋ⣬ǰһ�ٲ�ĺ���___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��������AEFG��һ��������A����G��E�ֱ����߶�AD��AB�ϣ�����������AEFG�Ƶ�A��˳ʱ�뷽����ת������DG������ת�Ĺ����У����ܷ��ҵ�һ���߶εij����߶�DG�ij���ʼ����ȣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��![]() �ڵ�һ���ޣ�����A��x�������ߣ�����Ϊ��B������OA��
�ڵ�һ���ޣ�����A��x�������ߣ�����Ϊ��B������OA��![]() ����M��O��������y�����������ÿ��2����λ���ȵ��ٶ��˶�����N�ӵ�B������ÿ��3����λ���ȵ��ٶ���x�Ḻ�����˶�����M���Nͬʱ���������M���˶�ʱ��Ϊt�룬����AM��AN��MN��
����M��O��������y�����������ÿ��2����λ���ȵ��ٶ��˶�����N�ӵ�B������ÿ��3����λ���ȵ��ٶ���x�Ḻ�����˶�����M���Nͬʱ���������M���˶�ʱ��Ϊt�룬����AM��AN��MN��
![]() ��a��ֵ��
��a��ֵ��
![]() ��
��![]() ʱ��
ʱ��
![]() ��̽��
��̽��![]() ��
��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
![]() ���ж��ı���AMON������Ƿ�仯�������仯���������ֵ�����仯����˵�����ɣ�
���ж��ı���AMON������Ƿ�仯�������仯���������ֵ�����仯����˵�����ɣ�
![]() ��
��![]() ʱ�������t��ֵ��
ʱ�������t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=2x+2��y�ύ��A�㣬�뷴�������� ![]() ��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO=2��
��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO=2��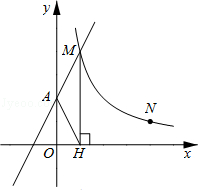
��1����k��ֵ��
��2����N��a��1���Ƿ��������� ![]() ��x��0��ͼ���ϵĵ㣬��x�����Ƿ���ڵ�P��ʹ��PM+PN��С�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��x��0��ͼ���ϵĵ㣬��x�����Ƿ���ڵ�P��ʹ��PM+PN��С�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com