
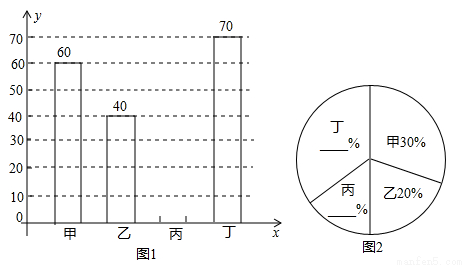
Ä³ÖŠŃ§æŖÕ¹”°ĀĢ»Æ¼ŅĻē”¢Ö²Ź÷ŌģĮÖ”±»ī¶Æ£¬ĪŖĮĖ½āČ«Š£Ö²Ź÷Ēéæö£¬¶ŌøĆŠ£¼×”¢ŅŅ”¢±ū”¢¶”ĖÄøö°ą¼¶Ö²Ź÷µÄæĆŹ÷ŗĶĖłÕ¼°Ł·Ö±ČĒéæö½ųŠŠĮĖµ÷²é£¬½«ŹÕ¼ÆµÄŹż¾ŻÕūĄķ²¢»ęÖĘ³ÉĶ¼1ŗĶĶ¼2Į½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ¼ÖŠµÄŠÅĻ¢£¬Ķź³ÉĻĀĮŠĪŹĢā£ŗ
£Ø1£©ÕāĖÄøö°ą¹²Ö²Ź÷””””æĆ£»
£Ø2£©Ēė²¹Č«Į½·łĶ³¼ĘĶ¼£»
£Ø3£©ČōĖÄøö°ą¼¶Ö²Ź÷µÄĘ½¾ł³É»īĀŹŹĒ95%£¬Č«Š£¹²Ö²Ź÷2000æĆ£¬ĒėÄć¹Ą¼ĘČ«Š£ÖÖÖ²µÄŹ÷ÖŠ³É»īµÄŹ÷“óŌ¼ÓŠ¶ąÉŁæĆ£æ
£Ø1£©200£»£Ø2£©²¹Č«Į½·łĶ³¼ĘĶ¼¼ū½āĪö£»£Ø3£©1900£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻŅŅ°ąÖ²Ź÷40æĆ£¬ĖłÕ¼±ČĪŖ20%£¬¼“æÉĒó³öÕāĖÄøö°ąÖÖŹ÷×ÜæĆŹż£ŗ40”Ā20%=200£ØæĆ£©£®
£Ø2£©øł¾Ż¶”°ąÖ²Ź÷70æĆ£¬×ÜæĆŹżŹĒ200£¬¼“æÉĒó³ö¶”ĖłÕ¼µÄ°Ł·Ö±Č£¬ŌŁÓĆÕūĢå1¼õČ„ĘäĖüĖłÕ¼µÄ°Ł·Ö±Č£¬¼“æÉµĆ³ö±ūĖłÕ¼µÄ°Ł·Ö±Č£¬ŌŁ³ĖŅŌ×ÜæĆŹż£¬¼“æÉµĆ³ö±ūÖ²Ź÷µÄæĆŹż£¬“Ó¶ų²¹Č«Ķ³¼ĘĶ¼£®
£Ø3£©ÓĆ×ÜæĆŹż”ĮĘ½¾ł³É»īĀŹ¼“æɵƵ½³É»īµÄŹ÷µÄæĆŹż£®
ŹŌĢā½āĪö£ŗ£Ø1£©200£®
£Ø2£©¶”ĖłÕ¼µÄ°Ł·Ö±ČŹĒ£ŗ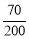 ”Į100%=35%£¬±ūĖłÕ¼µÄ°Ł·Ö±ČŹĒ£ŗ1©30%©20%©35%=15%£¬
”Į100%=35%£¬±ūĖłÕ¼µÄ°Ł·Ö±ČŹĒ£ŗ1©30%©20%©35%=15%£¬
±ūÖ²Ź÷µÄæĆŹżŹĒ£ŗ200”Į15%=30£ØæĆ£©£®
²¹Č«Į½·łĶ³¼ĘĶ¼ČēĻĀ£ŗ
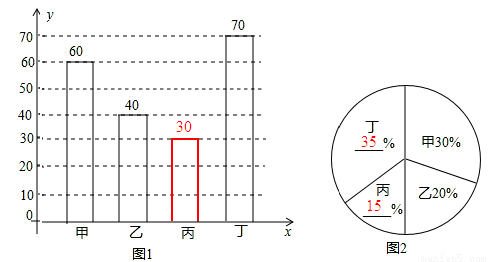
£Ø3£©øł¾ŻĢāŅāµĆ£ŗ2000”Į95%=1900£ØæĆ£©£¬
“š£ŗČ«Š£ÖÖÖ²µÄŹ÷ÖŠ³É»īµÄŹ÷ÓŠ1900æĆ£®
æ¼µć£ŗ1£®ĢõŠĪĶ³¼ĘĶ¼£»2£®ÉČŠĪĶ³¼ĘĶ¼£»3£®ĘµŹż”¢ĘµĀŹŗĶ×ÜĮæµÄ¹ŲĻµ£»4£®ÓĆŃł±¾¹Ą¼Ę×ÜĢ壮



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğ±±¾©ŹŠ²żĘ½ĒųÖŠæ¼Ņ»Ä£ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
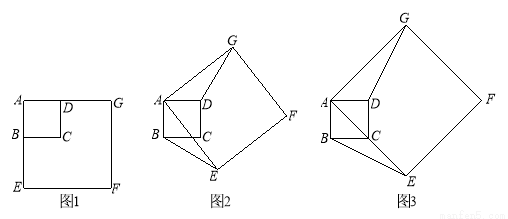
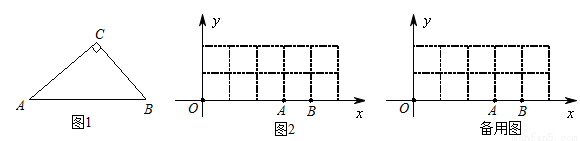
ČēĶ¼1£¬Õż·½ŠĪABCDÓėÕż·½ŠĪAEFGµÄ±ßAB”¢AE£ØAB£¼AE£©ŌŚŅ»ĢõÖ±ĻßÉĻ£¬Õż·½ŠĪAEFGŅŌµćAĪŖŠż×ŖÖŠŠÄÄꏱÕėŠż×Ŗ£¬É芿×Ŗ½ĒĪŖ . ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬Į½øöÕż·½ŠĪÖ»ÓŠµćAÖŲŗĻ£¬ĘäĖü¶„µć¾ł²»ÖŲŗĻ£¬Į¬½ÓBE”¢DG.
. ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬Į½øöÕż·½ŠĪÖ»ÓŠµćAÖŲŗĻ£¬ĘäĖü¶„µć¾ł²»ÖŲŗĻ£¬Į¬½ÓBE”¢DG.
£Ø1£©µ±Õż·½ŠĪAEFGŠż×ŖÖĮČēĶ¼2ĖłŹ¾µÄĪ»ÖĆŹ±£¬ĒóÖ¤£ŗBE=DG£»
£Ø2£©µ±µćCŌŚÖ±ĻßBEÉĻŹ±£¬Į¬½ÓFC£¬Ö±½ÓŠ“³ö”ĻFCD µÄ¶ČŹż£»
£Ø3£©ČēĶ¼3£¬Čē¹ū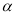 =45”ć£¬AB =2£¬AE=
=45”ć£¬AB =2£¬AE=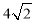 £¬ĒóµćGµ½BEµÄ¾ąĄė.
£¬ĒóµćGµ½BEµÄ¾ąĄė.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğ±±¾©ŹŠ²żĘ½ĒųÖŠæ¼Ņ»Ä£ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗŃ”ŌńĢā
ČēĶ¼ĖłŹ¾£¬Ä³³¬ŹŠŌŚŅ»Ā„ÖĮ¶žĀ„Ö®¼ä°²×°ÓŠµēĢŻ£¬Ģģ»Ø°åÓėµŲĆęĘ½ŠŠ. ÕÅĒææø×ÅĻä×Ó£ØČĖÓėĻä×ÓµÄ×Üø߶ČŌ¼ĪŖ2.2m£©³ĖµēĢŻøÕŗĆ°²Č«Ķعż£¬ĒėÄćøł¾ŻĶ¼ÖŠŹż¾Ż»Ų“š£¬Į½²ćĀ„Ö®¼äµÄøßŌ¼ĪŖ£Ø £©

A£®5.5m B. 6.2m C. 11 m D. 2.2 m
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğ±±¾©ŹŠ“óŠĖĒųÖŠæ¼Ņ»Ä£ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
Čē¹ūČż½ĒŠĪÓŠŅ»±ßÉĻµÄÖŠĻßĒ”ŗƵČÓŚÕā±ßµÄ³¤£¬ÄĒĆ“³ĘÕāøöČż½ĒŠĪĪŖ”°ŌČ³ĘČż½ĒŠĪ”±£®
£Ø1£©ŅŃÖŖ£ŗČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬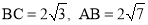 £®
£®
ĒóÖ¤£ŗ”÷ABCŹĒ”°ŌČ³ĘČż½ĒŠĪ”±£»
£Ø2£©ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxoyÖŠ£¬Čē¹ūČż½ĒŠĪµÄŅ»±ßŌŚxÖįÉĻ£¬ĒŅÕā±ßµÄÖŠĻßĒ”ŗƵČÓŚÕā±ßµÄ³¤£¬ĪŅĆĒÓÖ³ĘÕāøöČż½ĒŠĪĪŖ”°Ė®Ę½ŌČ³ĘČż½ĒŠĪ”±£®ČēĶ¼2£¬ĻÖÓŠ10øö±ß³¤ŹĒ1µÄŠ”Õż·½ŠĪ×é³ÉµÄ³¤·½ŠĪĒųÓņ¼ĒĪŖG, ĆæøöŠ”Õż·½ŠĪµÄ¶„µć³ĘĪŖøńµć£¬A£Ø3£¬0£©£¬B£Ø4£¬0£©£¬ČōC”¢D£ØC”¢DĮ½µćÓėO²»ÖŲŗĻ£©ŹĒxÖįÉĻµÄøńµć£¬ĒŅµćCŌŚµćAµÄ×ó²ą£®ŌŚGÄŚŹ¹”÷PACÓė”÷PBD¶¼ŹĒ”°Ė®Ę½ŌČ³ĘČż½ĒŠĪ”±µÄµćP¹²ÓŠ¼øøö£æĘäÖŠŹĒ·ń“ęŌŚŗį×ų±źĪŖÕūŹżµÄµćP£¬Čē¹ū“ęŌŚĒėĒó³öÕāøöµćPµÄ×ų±ź£¬Čē¹ū²»“ęŌŚĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğ±±¾©ŹŠ“óŠĖĒųÖŠæ¼Ņ»Ä£ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
Ēó²»µČŹ½×é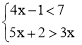 µÄÕūŹż½ā£®
µÄÕūŹż½ā£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğ±±¾©ŹŠ“óŠĖĒųÖŠæ¼Ņ»Ä£ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗŃ”ŌńĢā
ČōŅ»ĮŠ²»Č«ĪŖĮćµÄŹż³żĮĖµŚŅ»øöŹżŗĶ×īŗóŅ»øöŹżĶā£¬ĆæøöŹż¶¼µČÓŚĒ°ŗóÓėĖüĻąĮŚµÄĮ½ŹżÖ®ŗĶ£¬Ōņ³ĘÕāĮŠŹż¾ßÓŠ”°²Ø¶ÆŠŌÖŹ”±£®ŅŃÖŖŅ»ĮŠŹż¹²ÓŠ18øö£¬ĒŅ¾ßÓŠ”°²Ø¶ÆŠŌÖŹ”±£¬ŌņÕā18øöŹżµÄŗĶĪŖ£Ø £©
A£®-64 B£®0 C£®18 D£®64
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğ±±¾©ŹŠ·įĢØĒų֊漶žÄ£ŹżŃ§¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
ŅŃÖŖa2-2a-2=0£¬Ē󓜏żŹ½£Ø1-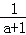 £©”Ā
£©”Ā µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2013-2014ѧğČĆɹžÅÄź¼¶6ŌĀÖŠæ¼Ä£ÄāŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
±±¾©°ĀŌĖ»įæŖÄ»Ē°£¬Ä³ĢåÓżÓĆĘ·ÉĢ³”Ō¤²āÄ³Ę·ÅĘŌĖ¶Æ·žÄܹ»³©Ļś£¬¾ĶÓĆ32000ŌŖ¹ŗ½ųĮĖŅ»ÅśÕāÖÖŌĖ¶Æ·ž£¬ÉĻŹŠŗóŗÜæģĶŃĻś£®ÉĢ³”ÓÖÓĆ68000ŌŖ¹ŗ½ųµŚ¶žÅśÕāÖÖŌĖ¶Æ·ž£¬Ėł¹»ŹżĮæŹĒµŚŅ»Åś¹ŗ½ųŹżĮæµÄ2±¶£¬µ«ĆæĢ×½ų¼Ū¶ąĮĖ10ŌŖ£®
£Ø1£©øĆÉĢ³”Į½“Ī¹²¹ŗ½ųÕāÖÖÅĘŌĖ¶Æ·ž¶ąÉŁĢ×£æ
£Ø2£©Čē¹ūÕāĮ½ÅśŌĖ¶Æ·žĆæĢ׵ďŪ¼ŪĻąĶ¬£¬ĒŅČ«²æŹŪĶźŗó×ÜĄūČóĀŹ²»µĶÓŚ20%£¬ÄĒĆ“ĆæĢ׏Ū¼ŪÖĮÉŁŹĒ¶ąÉŁŌŖ£æ£Ø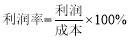 £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com