
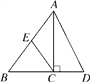
【题目】如图,在△ABD中,AC⊥BD于点C, ![]() ,点E是AB的中点,tanD=2,CE=1,求sin∠ECB的值和AD的长.
,点E是AB的中点,tanD=2,CE=1,求sin∠ECB的值和AD的长.
【答案】sin∠ECB=![]() , AD=
, AD=![]() .
.
【解析】试题分析:由直角三角形斜边上的中线等于斜边的一半,得到AB=2,设BC=3x,则CD=2x,AC=4x,在Rt△ACB中由勾股定理AB=5x,由∠ECB=∠B,求出sin∠ECB及x的值,在Rt△ACD中,由勾股定理求得AD的长.
试题解析:∵AC⊥BD,∴∠ACB=∠ACD=90°,∵点E是AB的中点,CE=1,∴BE=CE=1,AB=2CE=2,∴∠B=∠ECB,
∵![]() ,∴设BC=3x,CD=2x,
,∴设BC=3x,CD=2x,
在Rt△ACD中,tanD=2,∴ ![]() ,∴AC=4x,
,∴AC=4x,
在Rt△ACB中,由勾股定理得AB=![]() =5x,∴sin∠ECB=sinB=
=5x,∴sin∠ECB=sinB=![]() =
=![]() ,由AB=2,得x=
,由AB=2,得x=![]() ,
,
∴AD=![]() =
=![]() =2
=2 ![]() =2
=2![]() ×
×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点O叠放在一起.
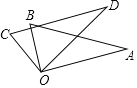
(1)如果∠BOD=60°,那么∠AOC= ,如果∠AOC=130°,那么∠BOD= .
(2)猜想∠AOC与∠BOD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,CD⊥AB于D,P是线段CD上一个动点,以P为直角顶点向下作等腰Rt△BPE,连结AE,DE.
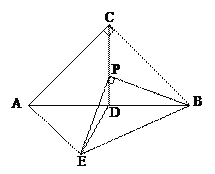
(1)∠BAE的度数是否为定值?若是,求出∠BAE的度数;
(2)直接写出DE的最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a,宽为2b的 长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形。

(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)S阴影= ;
(方法2)S阴影= ;
(3)观察如图2,写出(a+b)2、(a-b)2,ab三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决问题:若x+y=10,xy=16,求x-y的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)表示﹣3和2两点之间的距离是_____;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
如果|a+2|=3,那么a=_____;
(2)若数轴上表示数a的点位于﹣4与2之间,则|a+4|+|a﹣2|的值为_____;
(3)利用数轴找出所有符合条件的整数点x,使得|x+2|+|x﹣5|=7,这些点表示的数的和是_____;
(4)当a=_____时,|a+3|+|a﹣1|+|a﹣4|的值最小,最小值是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
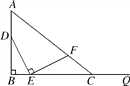
【题目】如图,AB=4,射线BQ和AB互相垂直,点D是AB上的一个动点,点E在射线BQ上,BE=![]() DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com