
����Ŀ��Ϊ������ȫ�������������У��Ż����л�������Լ��Դ��ij�й�����˾��������һ����10̨ȫ�µĻ�϶���������������A��B�����ͺţ�����ÿ̨�ļ۸���ʡ�������±���
A | B | |
�۸���Ԫ��̨�� | a | b |
��ʡ���������������꣩ | 2.4 | 2 |
�����飬����һ̨A�ͳ��ȹ���һ̨B�ͳ���10��Ԫ������3̨A�ͳ��ȹ���4̨B�ͳ���30��Ԫ��
��1�������a��b��ֵ��
��2��������������϶��������������ֳ��Ͷ�Ҫ�У�ÿ���ܽ�ʡ������������21.6�����������м��ֹ�����������д�������̣�
��3����2������ʡǮ�Ĺ�������������Ĺ����
���𰸡���1��a��b��ֵ�ֱ���70��60����2������6�ֹ��������������̼������� ��3������A�ͳ�4����B�ͳ�6��������Ĺ�������640��Ԫ��
��������
��1������������г�����a,b�ķ����飬�ⷽ���鼴�ɣ�
��2���蹺��A������x��������B��������10��x���������ݡ�����������϶��������������ֳ��Ͷ�Ҫ�У�ÿ���ܽ�ʡ������������21��6�������г�����ʽ���������ʽ��ͬʱע�����ֳ��Ͷ�Ҫ�У�����ȷ��x��ȡֵ��Χ��Ȼ�����xΪ��������ȷ��x��ȡֵ��6�֣�
��3���蹺����Ϊw��Ԫ������A�ͳ�x�����ȸ��������ҵ�w��x֮��Ĺ�ϵʽ��Ȼ�����һ�κ��������ʼ��ɵó���
��1��������ɵã�
![]() ����ã�
����ã�![]() ��
��
��a��b��ֵ�ֱ���70��60��
��2���蹺��A������x��������B��������10��x������
������ɵã�
2��4x+2��10��x����21��6����ã�x��4��
�����ֳ��Ͷ�Ҫ�У�
��![]() ��
��
��4��x��10��
��x������
��x=4��5��6��7��8��9��
���6�ֹ���������
��3���蹺����Ϊw��Ԫ������A�ͳ�x����������ɵã�
w=70x+60��10��x��=10x+600����4��x��10��x������
��10>0
��w��x�����������
�൱x=4ʱ��wȡ����Сֵ����ʱw��Сֵ=640����Ԫ����
�𣺣�2������ʡǮ�Ĺ���Ϊ������A�ͳ�4����B�ͳ�6��������Ĺ�������640��Ԫ��


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У�ֱ��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����
����![]() ��ƽ��
��ƽ��![]() ���ֱ��
���ֱ��![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ���߶�
���߶�![]() �ϣ��ӳ�
�ϣ��ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��
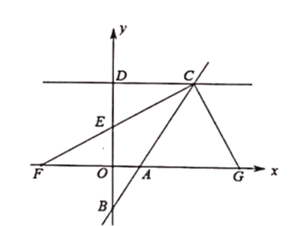
��1����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2������![]() ǡ����
ǡ����![]() �е�ʱ����
�е�ʱ����![]() �������
�������
��3���Ƿ����![]() ��ʹ��
��ʹ��![]() ��ֱ�������Σ������ڣ�ֱ��д��
��ֱ�������Σ������ڣ�ֱ��д��![]() ��ֵ;�������ڣ���˵�����ɣ�
��ֵ;�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��
(1)��֤������mΪ�κ�ʵ�����˺���ͼ����x�������������㣻
(2)���˺���ͼ����x���һ������Ϊ��-3��0������˺���ͼ����x�����һ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���EΪCD���е㣬����AE�ӳ���BC���ӳ����ڵ�F������BE��AE��FE��BE��AF��
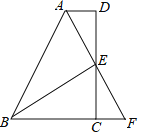
��1����֤����AED�ա�FEC
��2����֤��AB��BC��AD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij������ѵ���У�һ��Ա�ھ�������12�״����䣬����������2.4�ߵ����ź��������������е�·����������y=ax2+bx+c����ͼ���������ĸ����ۣ���a��b��0����a����![]() ���۩�
���۩�![]() ��a��0����0��b����12a��������ȷ�Ľ����ǣ�������
��a��0����0��b����12a��������ȷ�Ľ����ǣ�������
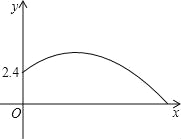
A. �٢� B. �٢� C. �ڢ� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��ӯ��45Ԫ��Ϊ���������ۡ�����ӯ��������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�4�������̳�ƽ��ÿ��ӯ��2100Ԫ��ÿ������Ӧ���۶���Ԫ��������������⣺
��1��δ����֮ǰ��ij�̳���������ӯ��Ϊ�� �� Ԫ��
��2�����ۺ���ij�̳�ÿ������Ӧ����xԪ����ÿ������ӯ���� ��Ԫ��ƽ��ÿ����۳��� �������ú�x�Ĵ���ʽ���б�ʾ��
��3�����г����̣����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �Ķ����ǣ� ��
�Ķ����ǣ� ��
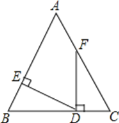
A.160��B.150��C.140��D.120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���д������( )
A ���ں���y����x2�У���x��0ʱy�����ֵ0
B���ں���y��2x2�У���x��0ʱy��x�����������
C��������y��2x2��y����x2��![]() �У�������y��2x2�Ŀ�����С��������y����x2�Ŀ������
�У�������y��2x2�Ŀ�����С��������y����x2�Ŀ������
D������a���������Ǹ�����������y��ax2�Ķ��㶼������ԭ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com