
【题目】某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
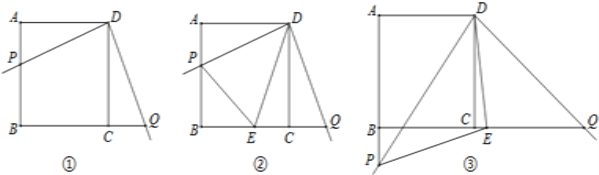
(1)求证:DP=DQ;
(2)如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
【答案】(1)见解析;(2)PE=QE,理由见解析;(3)![]()
【解析】
(1)证明△ADP≌△CDQ,即可得到结论:DP=DQ.
(2)证明△DEP≌△DEQ,即可得到结论:PE=QE.
(3)与(1)(2)同理,可以分别证明△ADP≌△CDQ、△DEP≌△DEQ.在Rt△BPE中,利用勾股定理求出PE(或QE)的长度,从而可求得![]() ,而△DEP≌△DEQ,所以S△DEP=S△DEQ=
,而△DEP≌△DEQ,所以S△DEP=S△DEQ=![]() .
.
解:(1)证明:
∵∠ADC=∠PDQ=90°,
∴∠ADP=∠CDQ.
在△ADP与△CDQ中,
∵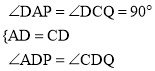 ,
,
∴△ADP≌△CDQ(ASA).
∴DP=DQ.
(2)猜测:PE=QE.
证明如下:
由(1)可知,DP=DQ.
在△DEP与△DEQ中,
∵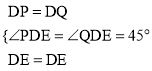 ,
,
∴△DEP≌△DEQ(SAS).
∴PE=QE.
(3)∵AB:AP=3:4,AB=6,
∴AP=8,BP=2.
与(1)同理,可以证明△ADP≌△CDQ,
∴CQ=AP=8.
与(2)同理,可以证明△DEP≌△DEQ
,∴PE=QE.
设QE=PE=x,则![]() .
.
在Rt△BPE中,由勾股定理得:BP2+BE2=PE2,即:![]() ,
,
解得:![]() ,即QE=
,即QE=![]() .
.
∴![]() .
.
∵△DEP≌△DEQ,
∴S△DEP=S△DEQ=![]() .
.


科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元; 如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元.
(1)求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3210元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
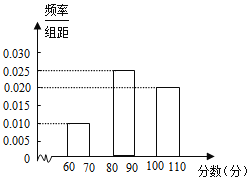
【题目】某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与作答《2020年新型冠状病毒肺炎的防护全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从该社区抽取40名居民的答卷,并对他们的成绩(单位:分)进行整理、分析,过程如下:
收集数据
85 65 95 100 90 95 85 65 75 85 100 90 70 90 100 80 80 100 95 75 80 100 80 95 65 100 90 95 85 80 100 75 60 90 70 80 95 75 100 90
整理数据(每组数据可含最低值,不含最高值)
分组(分) | 频数 | 频率 |
60~70 | 4 | 0.1 |
70~80 | a | b |
80~90 | 10 | 0.25 |
90~100 | c | d |
100~110 | 8 | 0.2 |
分析数据
(1)填空:a= ,b= ,c= ,d= ;
(2)补全频率分布直方图;
(3)由此估计该社区居民在线答卷成绩在 (分)范围内的人数最多;
(4)如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
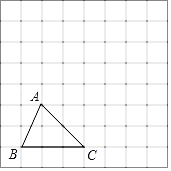
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,按要求完成下列步骤:
(1)画出将△ABC向上平移3个单位后得到的△A1B1C1;
(2)画出将△A1B1C1绕点C1按顺时针方向旋转90°后所得到的△A2B2C1.
(3)求出第(2)问中B1点经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中∠A=∠ABC=90°,点E是CD的中点,△ABD与 △EBD关于直线BD对称,![]() ,
,![]() .
.
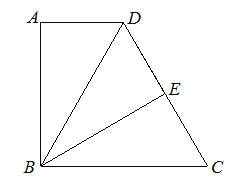
(1)求点A和点E之间的距离;
(2)联结AC交BE于点F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
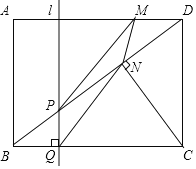
【题目】如图,在矩形ABCD中,CD=3cm,BC=4cm,连接BD,并过点C作CN⊥BD,垂足为N,直线l垂直BC,分别交BD、BC于点P、Q.直线l从AB出发,以每秒1cm的速度沿BC方向匀速运动到CD为止;点M沿线段DA以每秒1cm的速度由点D向点A匀速运动,到点A为止,直线1与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;
(2)连接PM和QN,当四边形MPQN为平行四边形时,求t的值;
(3)在整个运动过程中,当t为何值时△PMN的面积取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
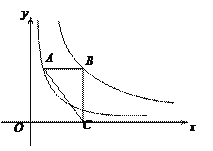
A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com