
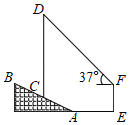
ЁОЬтФПЁПШчЭМЃЌЮЊМгПь5GЭјТчНЈЩшЃЌФГЭЈаХЙЋЫОдквЛИіЦТЖШiЃН1ЃК2.4ЕФЩНЦТABЩЯНЈСЫвЛзљаХКХЫўCDЃЌаХКХЫўЕзЖЫCЕНЩННХAЕФОрРыACЃН13УзЃЌдкОрЩННХAЫЎЦНОрРы18УзЕФEДІЃЌгавЛИпЖШЮЊ10УзЕФНЈжўЮяEFЃЌдкНЈжўЮяЖЅЖЫFДІВтЕУаХКХЫўЖЅЖЫDЕФбіНЧЮЊ37ЁуЃЈаХКХЫўМАЩНЦТЕФЦЪУцКЭНЈжўЮяЕФЦЪУцдкЭЌвЛЦНУцЩЯЃЉЃЌдђаХКХЫўCDЕФИпЖШдМЪЧЃЈЁЁЁЁЃЉЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЉ
A.22.5УзB.27.5УзC.32.5УзD.45.0Уз
ЁОД№АИЁПB
ЁОНтЮіЁП
Й§ЕуFзїFHЁЭDCгкЕуHЃЌбгГЄDCНЛEAгкЕуGЃЌПЩЕУЫФБпаЮEFHGЪЧОиаЮЃЌИљОнABЕФЦТЖШiЃН1ЃК2.4ЃЌACЃН13ЃЌПЩЕУCGЃН5ЃЌAGЃН12ЃЌCHЃНGHЉCGЃН10Љ5ЃН5ЃЌдйИљОнШёНЧШ§НЧКЏЪ§МДПЩЧѓГіаХКХЫўCDЕФИпЖШЃЎ
НтЃКШчЭМЃЌЙ§ЕуFзїFHЁЭDCгкЕуHЃЌ
бгГЄDCНЛEAгкЕуGЃЌ
дђЫФБпаЮEFHGЪЧОиаЮЃЌ
ЁрFHЃНGEЃЌCGЃНEFЃЌ
ЁпABЕФЦТЖШiЃН1ЃК2.4ЃЌACЃН13ЃЌ
ЁрCGЃН5ЃЌAGЃН12ЃЌ
ЁрCHЃНGHЉCGЃН10Љ5ЃН5ЃЌ
ЁрGEЃНAG+AEЃН12+18ЃН30ЃЌ
ЁрдкRtЁїDCFжаЃЌЁЯDFCЃН37ЁуЃЌFHЃНGEЃН30ЃЌ
ЁрDHЃНFHtan37ЁуЁж30ЁС0.75Ёж22.5ЃЌ
ЁрCDЃНDH+CHЁж22.5+5Ёж27.5ЃЈУзЃЉЃЎ
ЫљвдаХКХЫўCDЕФИпЖШдМЪЧ27.5УзЃЎ
ЙЪбЁЃКBЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
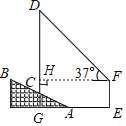
ЁОЬтФПЁПШчЭМЃЌЁбOжаЃЌABЪЧЁбOЕФжБОЖЃЌGЮЊЯвAEЕФжаЕуЃЌСЌНгOGВЂбгГЄНЛЁбOгкЕуDЃЌСЌНгBDНЛAEгкЕуFЃЌбгГЄAEжСЕуCЃЌЪЙЕУFC=BCЃЌСЌНгBCЃЎ
(1)ЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
(2)ЁбOЕФАыОЖЮЊ5ЃЌtanA=![]() ЃЌЧѓFDЕФГЄЃЎ
ЃЌЧѓFDЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
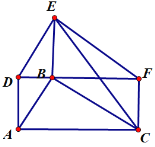
ЁОЬтФПЁПШчЭМЃЌЁїDEFгЩЁїABCЦНвЦЕУЕНЃЌЁЯDFE=ЁЯCDF=30ЁуЃЌЁЯDEF=90ЁуЃЌBEЁЭDFгкЕуBЃЎСЌНгCEЃЌAB=3ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮACDFЮЊОиаЮ
ЃЈ2ЃЉЧѓЯпЖЮCEЕФГЄКЭЁїCEFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЎЕу
ЃЎЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЗНЯђвдУПУы
ЗНЯђвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕу![]() дЫЖЏЃЈЕу
дЫЖЏЃЈЕу![]() ВЛгы
ВЛгы![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() НЛелЯп
НЛелЯп![]() гкЕу
гкЕу![]() вд
вд![]() ЮЊБпЮЪЯТзїе§ЗНаЮ
ЮЊБпЮЪЯТзїе§ЗНаЮ![]() Еу
Еу![]() ТфдкБп
ТфдкБп![]() ЩЯЩшЕу
ЩЯЩшЕу![]() дЫЖЏЕФЪБМфЮЊ
дЫЖЏЕФЪБМфЮЊ![]() ЃЈУыЃЉЃЎ
ЃЈУыЃЉЃЎ

ЃЈ1ЃЉжБНггУКЌ![]() ЕФДњЪ§ЪНБэЪОЯпЖЮ
ЕФДњЪ§ЪНБэЪОЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ2ЃЉЕБЕу![]() ТфдкБп
ТфдкБп![]() ЩЯЪБЃЌЧѓ
ЩЯЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЕБе§ЗНаЮ![]() гы
гы![]() жиЕўВПЗжЭМаЮЮЊЫФБпаЮЪБЃЌЩшЫФБпаЮЕФУцЛ§ЮЊ
жиЕўВПЗжЭМаЮЮЊЫФБпаЮЪБЃЌЩшЫФБпаЮЕФУцЛ§ЮЊ![]() ЃЈЦНЗНЕЅЮЛЃЉЃЌЧѓ
ЃЈЦНЗНЕЅЮЛЃЉЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ4ЃЉЕу![]() ЮЊБп
ЮЊБп![]() ЕФжаЕуЃЌжБНгаДГіжБЯп
ЕФжаЕуЃЌжБНгаДГіжБЯп![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§БШЮЊ
ЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§БШЮЊ![]() ЪБ
ЪБ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
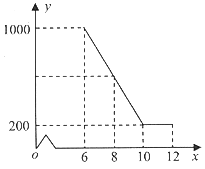
ЁОЬтФПЁПФГзЄДхЗіЦЖаЁзщЪЕЪЉВњвЕЗіЦЖЃЌАяжњЦЖРЇХЉЛЇНјааЮїЙЯжжжВКЭЯњЪл.вбжЊЮїЙЯЕФГЩБОЮЊ6дЊ/ЧЇПЫЃЌЙцЖЈЯњЪлЕЅМлВЛЕЭгкГЩБОЃЌгжВЛИпгкГЩБОЕФСНБЖ.ОЙ§ЪаГЁЕїВщЗЂЯжЃЌФГЬьЮїЙЯЕФЯњЪлСПy(ЧЇПЫ)гыЯњЪлЕЅМлx(дЊ/ЧЇПЫ)ЕФКЏЪ§ЙиЯЕШчЯТЭМЫљЪОЃК
(1)ЧѓyгыxЕФКЏЪ§НтЮіЪН(вВГЦЙиЯЕЪН)ЃЛ
(2)ЧѓетвЛЬьЯњЪлЮїЙЯЛёЕУЕФРћШѓЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌABЃН2ЃЌЁЯABCЃН45ЁуЃЌЕуEЮЊЩфЯпADЩЯвЛЖЏЕуЃЌСЌНгBEЃЌНЋBEШЦЕуBФцЪБеыа§зЊ60ЁуЕУЕНBFЃЌСЌНгAFЃЌдђAFЕФзюаЁжЕЪЧ_____ЃЎ
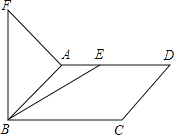
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЕуEЮЊЯпЖЮBOЩЯвЛЕуЃЌСЌНгCEЃЌНЋCEШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНCFЃЌСЌНгEFНЛCDгкЕуGЃЎ
ЃЈ1ЃЉШєABЃН4ЃЌBEЃН![]() ЃЌЧѓЁїCEFЕФУцЛ§ЃЎ
ЃЌЧѓЁїCEFЕФУцЛ§ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЯпЖЮFEЕФбгГЄЯпНЛABгкЕуHЃЌЙ§ЕуFзїFMЁЭCDгкЕуMЃЌЧѓжЄЃКBH+MGЃН![]() BEЃЛ
BEЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕуEЮЊЩфЯпODЩЯвЛЕуЃЌЯпЖЮFEЕФбгГЄЯпНЛжБЯпCDгкЕуGЃЌНЛжБЯпABгкЕуHЃЌЙ§ЕуFзїFMДЙжБжБЯпCDгкЕуMЃЌЧыжБНгаДГіЯпЖЮBHЁЂMGЁЂBEЕФЪ§СПЙиЯЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() вдЕу
вдЕу![]() ЮЊдВаФЃЌвдШЮвтГЄЮЊАыОЖзїЛЁЗжБ№НЛ
ЮЊдВаФЃЌвдШЮвтГЄЮЊАыОЖзїЛЁЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гк
гк![]() СНЕуЃЌдйЗжБ№вдЕу
СНЕуЃЌдйЗжБ№вдЕу![]() ЮЊдВаФЃЌвдДѓгк
ЮЊдВаФЃЌвдДѓгк![]() ЕФГЄЮЊАыОЖзїЛЁНЛгкЕу
ЕФГЄЮЊАыОЖзїЛЁНЛгкЕу![]() ЃЌзїЩфЯп
ЃЌзїЩфЯп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌдђОиаЮ
ЃЌдђОиаЮ![]() ЕФУцЛ§ЕШгк__________ЃЎ
ЕФУцЛ§ЕШгк__________ЃЎ
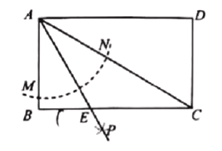
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкДѓТЅABЕФе§ЧАЗНгавЛаБЦТCDЃЌCD=4УзЃЌЦТНЧЁЯDCE=30ЁуЃЌаЁКьдкаБЦТЯТЕФЕуCДІВтЕУТЅЖЅBЕФбіНЧЮЊ60ЁуЃЌдкаБЦТЩЯЕФЕуDДІВтЕУТЅЖЅBЕФбіНЧЮЊ45ЁуЃЌЦфжаЕуAЁЂCЁЂEдкЭЌвЛжБЯпЩЯЃЎ

ЃЈ1ЃЉЧѓаБЦТCDЕФИпЖШDEЃЛ
ЃЈ2ЃЉЧѓДѓТЅABЕФИпЖШЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com