
 如图,直线l上依次有三个点O,A,B,OA=40cm,OB=160cm.
如图,直线l上依次有三个点O,A,B,OA=40cm,OB=160cm.分析 (1)①P、Q间的距离=|160-它们各自运动的距离|;
②需要对点P的两个不同位置进行分类讨论:点P在点B的左边和点P在点B的右边;
(2)此题就可把它当成一个静止的线段问题来解决了,但必须借助图形.
解答  解:(1)①依题意得,PQ=|160-5t|;
解:(1)①依题意得,PQ=|160-5t|;
故答案是:|160-5t|;
②如图1所示:4t-40=2(160-4t),
解得 t=30,
则点Q的运动速度为:$\frac{60}{30}$=2(cm/s);
如图2所示:4t-40=2(4t-160),
解得t=7,
则点Q的运动速度为:$\frac{60}{70}$=$\frac{6}{7}$(cm/s);
综上所述,点Q的运动速度为2cm/s或$\frac{6}{7}$cm/s;
(2)如图3,两点P,Q分别在线段OA,AB上,分别取OQ和BP的中点M,N,求$\frac{OP+BQ}{MN}$的值.
OP=x BQ=y,则MN=$\frac{1}{2}$(160-x)-$\frac{1}{2}$(160-y)+x=$\frac{1}{2}$(x+y),
所以,$\frac{OP+BQ}{MN}$=$\frac{x+y}{\frac{1}{2}(x+y)}$=2.
点评 本题考查了一元一次方程的应用.做这类题时学生一定要认真仔细地阅读,利用已知条件求出未知值.学生平时就要培养自己的思维能力.而且要图形结合,与生活实际联系起来,也可以把此题当成一道路程题来对待.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
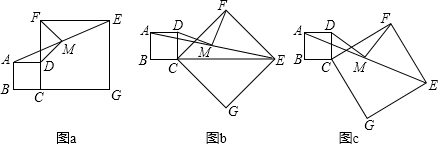
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=$\frac{\sqrt{5}}{4}$;④S△DEF=4$\sqrt{5}$,其中正确结论的个数是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=$\frac{\sqrt{5}}{4}$;④S△DEF=4$\sqrt{5}$,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有七张相同的纸条,恰好组成一个正方形,每张纸条上都依次写上1~7这七个数字,现在要把这些字条剪短后,左右对调(不能上下对调)仍拼成一个正方形,并使正方形的每一行,每一列及两条对角线上的7个数之和都相等.请你开动脑筋,看看能不能想出以剪最少块数的方法达到以上要求.
有七张相同的纸条,恰好组成一个正方形,每张纸条上都依次写上1~7这七个数字,现在要把这些字条剪短后,左右对调(不能上下对调)仍拼成一个正方形,并使正方形的每一行,每一列及两条对角线上的7个数之和都相等.请你开动脑筋,看看能不能想出以剪最少块数的方法达到以上要求.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
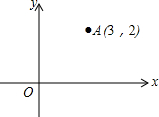 如图,在平面直角坐标系中,点A的坐标为(3,2),能否建立一个新的平面直角坐标系x′O′y′,使得在新的x′O′y′中,点O的坐标变为(-3,-2)?如果可以,请画出新的坐标系;若不可以,请说明理由.
如图,在平面直角坐标系中,点A的坐标为(3,2),能否建立一个新的平面直角坐标系x′O′y′,使得在新的x′O′y′中,点O的坐标变为(-3,-2)?如果可以,请画出新的坐标系;若不可以,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com