一个三位自然数正好等于它各数位上的数字和的18倍.这个三位自然数是?
【答案】
分析:设这个自然数的百位,十位,个位上的数字分别为A、B、C,先根据这个三位自然数正好等于它各数位上的数字和的18倍,列出方程100A+10B+C=18(A+B+C),整理后得:82A=8B+17C,再根据此等式及自然数的组成规律确定A、B、C的取值范围,进而分析验证即可.
解答:解:设这个自然数的百位,十位,个位上的数字分别为A、B、C,由题意得:
100A+10B+C=18(A+B+C),
化简得:82A=8B+17C.
∵0≤B≤9,0≤C≤9,
∴82A=8B+17C≤8×9+17×9=225,
∴A≤2
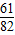
,
又∵A是正整数,
∴A=1或2.
①当A=1时,得82=8B+17C,
∵B、C都是自然数,
∴B=6,C=2;
②当A=2时,得164=8B+17C,
∵B、C都是自然数,
∴B=12,C=4,
∵B≤9,
∴B=12不合题意,舍去.
答:这个三位数是162.
点评:本题考查了数的整除性问题,属于竞赛题型,有一定难度.根据题意列出方程,然后进行分析整理是解答本题的关键.

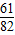 ,
,

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案